题目内容
3.全称命题“?x∈R,x2+5x>4”的否定是( )| A. | ?x0∈R,x2+5x>4 | B. | “?x∈R,x2+5x≤4 | C. | ?x0∈R,x2+5x≤4 | D. | 以上都不正确 |
分析 直接利用全称命题的否定是特称命题,写出结果即可.
解答 解:因为全称命题的否定是特称命题,所以,全称命题“?x∈R,x2+5x>4”的否定是:?x0∈R,x2+5x≤4.
故选:C.
点评 本题考查命题的否定,全称命题与特称命题的否定关系,是基础题.

练习册系列答案
相关题目
14.已知函数f(x)=sinπx和函数g(x)=cosπx在区间[-1,2]上的图象交于 A、B、C三点,则△ABC的面积是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{3\sqrt{2}}}{4}$ | C. | $\sqrt{2}$ | D. | $\frac{{5\sqrt{2}}}{4}$ |
8.为了了解某天甲乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14和5件,测量产品中的微量元素x,y的含量(单位:毫克).当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品.已知甲厂该天生产的产品共有98件,如表是乙厂的5件产品的测量数据:
(I)求乙厂该天生产的产品数量;
(Ⅱ)从乙厂抽出取上述5件产品中,随机抽取2件,求抽取的2件产品中优等品至少有1件的概率.
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
(Ⅱ)从乙厂抽出取上述5件产品中,随机抽取2件,求抽取的2件产品中优等品至少有1件的概率.
10.已知点A,B,C在圆O:x2+y2=2上运动,且AB⊥BC,若点P的坐标为(1,1),则|$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$|的取值范围是( )
| A. | [0,4$\sqrt{2}$] | B. | [2,4] | C. | [2$\sqrt{2}$,4$\sqrt{2}$] | D. | [2$\sqrt{2}$,3$\sqrt{2}$] |
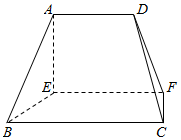 在如图所示的几何体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EE∥BC,BC=2AD=4,EF=3,AE=BE=2,则该几何体的体积为6.
在如图所示的几何体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EE∥BC,BC=2AD=4,EF=3,AE=BE=2,则该几何体的体积为6. .
. 的值域;
的值域; 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知 为锐角,
为锐角,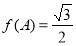 ,
, ,
, ,求
,求 的值.
的值.