题目内容
18.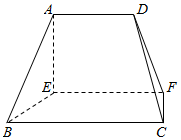 在如图所示的几何体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EE∥BC,BC=2AD=4,EF=3,AE=BE=2,则该几何体的体积为6.
在如图所示的几何体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EE∥BC,BC=2AD=4,EF=3,AE=BE=2,则该几何体的体积为6.
分析 把多面体的体积看作是三棱锥D-ABE与四棱锥D-BCFE的体积和,然后结合已知条件求解.
解答  解:由EF⊥平面AEB,且EF?平面BCFE
解:由EF⊥平面AEB,且EF?平面BCFE
得平面ABE⊥平面BCFE,又AE⊥EB,
∴AE⊥平面BCFE,
再由EF⊥平面AEB,AD∥EF,可得AD⊥平面AEB,
∴VD-AEB=$\frac{1}{3}$×$\frac{1}{2}$AE•DE•AD=$\frac{1}{6}$×2×2×2=$\frac{4}{3}$;
VD-BCFE=$\frac{1}{3}$SBCEF•AE=$\frac{1}{3}$×$\frac{1}{2}$(3+4)×2×2=$\frac{14}{3}$.
∴多面体的体积为VD-AEB+VD-BCEF=$\frac{4}{3}+\frac{14}{3}=6$.
故答案为:6.
点评 本题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

练习册系列答案
相关题目
9.设复数z满足(1+i)z=2i,其中i为虚数单位,则z的共轭复数$\overline{z}$=( )
| A. | -1+i | B. | -1-i | C. | 1+i | D. | 1-i |
6.已知数列{an}其通项公式为an=3n2-22n-1,则此数列中最小项为第( )项.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
3.全称命题“?x∈R,x2+5x>4”的否定是( )
| A. | ?x0∈R,x2+5x>4 | B. | “?x∈R,x2+5x≤4 | C. | ?x0∈R,x2+5x≤4 | D. | 以上都不正确 |
10.在伸缩变换$\left\{\begin{array}{l}{x′=3x}\\{y′=y}\end{array}\right.$的作用后,点(1,2)的坐标变为( )
| A. | (3,2) | B. | (1,2) | C. | ($\frac{1}{3}$,2) | D. | (1,$\frac{2}{3}$) |
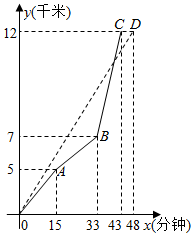 如图,在一次自行车越野赛中,甲,乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线( OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是0<x<38.
如图,在一次自行车越野赛中,甲,乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线( OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是0<x<38.