题目内容
8.为了了解某天甲乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14和5件,测量产品中的微量元素x,y的含量(单位:毫克).当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品.已知甲厂该天生产的产品共有98件,如表是乙厂的5件产品的测量数据:| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
(Ⅱ)从乙厂抽出取上述5件产品中,随机抽取2件,求抽取的2件产品中优等品至少有1件的概率.
分析 (Ⅰ)有分层抽样可知各层抽取的比例相等,先计算出甲厂抽取的比例,按此比例计算乙厂生产的产品总数即可.
(Ⅱ)先列举出所有的基本事件有10种等可能的结果,找到满足条件的基本事件的事件有7种,根据古典概型的概率公式计算即可.
解答 解:(Ⅰ)甲厂抽取的比例$\frac{14}{98}$,因为乙厂抽出5件,故乙厂生产的产品总数35件.
(Ⅱ)从编号为1,2,3,4,5的5件产品中任取2件共有10种等可能的结果.分别是(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)
设只有2号和5号产品是优等品,被抽中有以下7种:(1,2),(1,5),(2,3),(2,4),(2,5),(3,5),(4,5).
∴抽取的2件产品中优等品至少有1件的概率P=$\frac{7}{10}$.
点评 本题考查了分层抽样方法,独立事件的概率计算,考查了用样本的数据估计总体,解题的关键是读懂题意.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若函数$f(x)={log_{\frac{1}{3}}}x+\frac{1}{x}+a$的零点在区间(1,+∞)上,则实数a的取值范围是( )
| A. | (-∞,0) | B. | (-∞,-1) | C. | (-1,+∞) | D. | (0,+∞) |
19.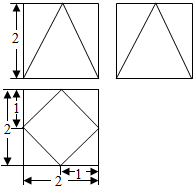 一个正方体截去四个角得到一个多面体,其三视图如图所示,则该多面体的体积为( )
一个正方体截去四个角得到一个多面体,其三视图如图所示,则该多面体的体积为( )
 一个正方体截去四个角得到一个多面体,其三视图如图所示,则该多面体的体积为( )
一个正方体截去四个角得到一个多面体,其三视图如图所示,则该多面体的体积为( )| A. | 4 | B. | $\frac{20}{3}$ | C. | $\frac{4}{3}$(3+$\sqrt{2}$) | D. | $\frac{16}{3}$ |
16.若在平面直角坐标中,方程x2+2xsinxy+1=0所表示的图形为( )
| A. | 直线 | B. | 抛物线 | C. | 一个点 | D. | 以上都不对 |
3.全称命题“?x∈R,x2+5x>4”的否定是( )
| A. | ?x0∈R,x2+5x>4 | B. | “?x∈R,x2+5x≤4 | C. | ?x0∈R,x2+5x≤4 | D. | 以上都不正确 |
13.已知a,b∈R,则“ab≥2”是“a2+b2≥4”成立的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
20.投掷两枚质地均匀的骰子,其向上的点数分别记为a,b,则直线ax-y+a-b=0在y轴上截距大于在x轴上截距的概率为( )
| A. | $\frac{5}{12}$ | B. | $\frac{5}{18}$ | C. | $\frac{5}{6}$ | D. | $\frac{5}{36}$ |
15.一个与正整数n有关的命题,当n=2时命题成立,且由n=k时命题成立可以推得n=k+2时命题也成立,则( )
| A. | 该命题对于n>2的自然数n都成立 | B. | 该命题对于所有的正偶数都成立 | ||
| C. | 该命题何时成立与k取值无关 | D. | 以上答案都不对 |
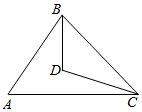 如图,D为△ABC内一点,并且满足AB=CD=4,∠A+∠BDC=180°,试确定S△ABC-S△BDC的最大值.
如图,D为△ABC内一点,并且满足AB=CD=4,∠A+∠BDC=180°,试确定S△ABC-S△BDC的最大值.