题目内容
已知f（x）为奇函数，g（x）为偶函数，且f（x）+g（x）=
，则f（3）=（ ）
| 1 |
| x-1 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：根据函数的奇偶性列出f（3）与g（3）的方程组，利用奇偶性化简后解之即可．
解答：
解：由已知得
，
又因为f（x）为奇函数，g（x）为偶函数，所以f（-3）=-f（3），g（-3）=g（3）．
代入方程组解得f（3）=
．
故选C
|
又因为f（x）为奇函数，g（x）为偶函数，所以f（-3）=-f（3），g（-3）=g（3）．
代入方程组解得f（3）=
| 3 |
| 8 |
故选C
点评：本题考查了利用函数的奇偶性求函数值的方法，一般是设而不求，整体代换．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知双曲线x2-
=1（b＞0）的一条渐近线的方程为y=2x，则b的值等于（ ）
| y2 |
| b2 |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |
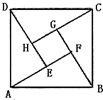一次在北京召开的国际数学家大会，会标如图所示，它是由4个相同的直角三角形与中间的小正方形拼成的一个大正方形，大正方形的面积是1，小正方形的面积是