题目内容
将6位志愿者分配到甲、已、丙3个志愿者工作站,每个工作站2人,由于志愿者特长不同,A不能去甲工作站,B只能去丙工作站,则A、B不在同一工作站的概率是 .
考点:古典概型及其概率计算公式
专题:概率与统计
分析:利用分步计算原理,根据特殊元素优先安排的原则,首先求出A不能去甲工作站,B只能去丙工作站的种数,再求出A、B不在同一工作站,根据概率公式计算即可.
解答:
解:根据A不能去甲工作站,B只能去丙工作站,所以甲站只能从余下的4人中任选2人,有
=6种,
每个工作站2人,所以丙站只能从余下的3人中,任选1人有
=3种,余下的两人到乙站,
不同的分配方法共有6×3=18种.
A、B在同一工作站,则只能是丙站,有
=6种,
故A、B不在同一工作站的种数为18-6=12,
故A、B不在同一工作站的概率是P=
=
.
故答案为:
| C | 2 4 |
每个工作站2人,所以丙站只能从余下的3人中,任选1人有
| C | 1 3 |
不同的分配方法共有6×3=18种.
A、B在同一工作站,则只能是丙站,有
| C | 2 4 |
故A、B不在同一工作站的种数为18-6=12,
故A、B不在同一工作站的概率是P=
| 12 |
| 18 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题主要考查了排列组合的问题以及古典概型的概率问题,关键是求出满足条件的种数,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6人站成一排,甲、乙、丙3个人不能都站在一起的排法种数为( )
| A、720 | B、144 |
| C、576 | D、684 |
已知复数z满足|z-i-1|+|z+i-1|=2,则z在复平面内对应的点的轨迹是( )
| A、线段 | B、圆 | C、椭圆 | D、抛物线 |
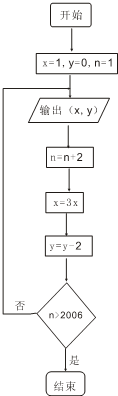 已知某算法的流程图如图示,若将输出的(x,y)依次记为(x1,y1),(x2,y2),…,(xn,yn),…
已知某算法的流程图如图示,若将输出的(x,y)依次记为(x1,y1),(x2,y2),…,(xn,yn),…