题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,右焦点F(1,0).设O为坐标原点,M是直线l:x=2上的动点,过点F作OM的垂线与以OM为直径的圆D交于P、Q两点,则PO= .
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:用点斜式写出FP的方程,再由OP⊥PM,斜率之积等于-1得到一个等式,把FP的方程代入等式化简,可得x2+y2=2,即可求出线段PO的长.
解答:
 解:设点M(2,m),
解:设点M(2,m),
∵F(1,0)
∴FP的方程为:y-0=
(x-1)①,
∵过点F作OM的垂线与以OM为直径的圆交于点P,
∴OP⊥PM,∴kOP•kPM=-1,
即
•
=-1,∴x2+y2=2x+my ②,
把①代入②得:x2+y2=2x+my=2x+m•
(x-1)=2,
∴|OP|=
=
.
故答案为:
.
 解:设点M(2,m),
解:设点M(2,m),∵F(1,0)
∴FP的方程为:y-0=
| -2 |
| m |
∵过点F作OM的垂线与以OM为直径的圆交于点P,
∴OP⊥PM,∴kOP•kPM=-1,
即
| y |
| x |
| y-m |
| x-2 |
把①代入②得:x2+y2=2x+my=2x+m•
| -2 |
| m |
∴|OP|=
| x2+y2 |
| 2 |
故答案为:
| 2 |
点评:本题考查椭圆的方程、直线和圆的位置关系的应用,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
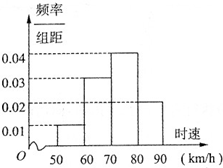 某地区对某路段公路上行驶的汽车速度实施监控,从中抽取50辆汽车进行测速分析,得到如图所示的时速的频率分布直方图,根据该图,时速在70km/h以下的汽车有
某地区对某路段公路上行驶的汽车速度实施监控,从中抽取50辆汽车进行测速分析,得到如图所示的时速的频率分布直方图,根据该图,时速在70km/h以下的汽车有