题目内容
已知从A口袋中摸出一个球是红球的概率为
，从B口袋中摸出一个球是红球的概率为
．现从两个口袋中各摸出一个球，那么这两个球中没有红球的概率是（ ）
| 1 |
| 3 |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题：概率与统计
分析：由题意可得，从A口袋中摸出一个球不是红球的概率为
，从A口袋中摸出一个球不是红球的概率为
，再把这两个概率相乘，即得所求．
| 2 |
| 3 |
| 3 |
| 5 |
解答：
解：由题意可得，从A口袋中摸出一个球不是红球的概率为
，从A口袋中摸出一个球不是红球的概率为
，
故从两个口袋中各摸出一个球，那么这两个球中没有红球的概率为
×
=
，
故选：B．
| 2 |
| 3 |
| 3 |
| 5 |
故从两个口袋中各摸出一个球，那么这两个球中没有红球的概率为
| 2 |
| 3 |
| 3 |
| 5 |
| 2 |
| 5 |
故选：B．
点评：本题主要考查相互独立事件的概率乘法公式，所求的事件的概率与它的对立事件的概率之间的关系，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中，“cosA=cosB”是“sinA=sinB”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
计算定积分
xdx=（ ）
| ∫ | 2 0 |
| A、2 | B、1 | C、4 | D、-2 |
命题“对任意实数x，都有x＞1”的否定是（ ）
| A、对任意实数x，都有x＜1 |
| B、不存在实数x，使x≤1 |
| C、对任意实数x，都有x≤1 |
| D、存在实数x，使x≤1 |
已知函数f（x）=m2-2cosx•m-sin2x在cosx=-1时取得最大值，在cosx=m时取得最小值，则实数m的取值范围为（ ）
| A、m≤-1 | B、m≥1 |
| C、0≤m≤1 | D、-1≤m≤0 |
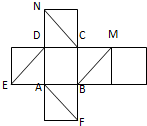如图是正方体的平面展开图，在这个正方体中；（1）CN与AF平行；
（2）CN与BE是异面直线；
（3）CN与BM成60°；
（4）DE与BM垂直．
以上四个命题中，正确命题的序号是（ ）
| A、（1）（2）（3） |
| B、（2）（4） |
| C、（3）（4） |
| D、（3） |
