题目内容
函数f(x)是定义在R上的偶函数,对于任意的实数x,都有f(x)•f(x+1)=1,则f(
)= .
| 7 |
| 2 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:要用递推的方法,用赋值法求得.
解答:
解:∵f(x)•f(x+1)=1
令x=-
,
则f(-
)•f(-
+1)=1,
∴f(-
)•f(
)=1,
∵函数f(x)是定义在R上的偶函数,
∴f(
)•f(
)=1
∴f(
)=±1,
再令x=
,
则f(
)•f(
)=1,
∴f(
)=±1,
再令x=
,
则f(
)•f(
)=1,
∴f(
)=±1,
再令x=
,
f(
)•f(
)=1
∴f(
)=±1,
故答案为:±1
令x=-
| 1 |
| 2 |
则f(-
| 1 |
| 2 |
| 1 |
| 2 |
∴f(-
| 1 |
| 2 |
| 1 |
| 2 |
∵函数f(x)是定义在R上的偶函数,
∴f(
| 1 |
| 2 |
| 1 |
| 2 |
∴f(
| 1 |
| 2 |
再令x=
| 1 |
| 2 |
则f(
| 1 |
| 2 |
| 3 |
| 2 |
∴f(
| 3 |
| 2 |
再令x=
| 3 |
| 2 |
则f(
| 3 |
| 2 |
| 5 |
| 2 |
∴f(
| 5 |
| 2 |
再令x=
| 5 |
| 2 |
f(
| 5 |
| 2 |
| 7 |
| 2 |
∴f(
| 7 |
| 2 |
故答案为:±1
点评:本题主要考查利用函数的主条件用递推的方法求函数值,这类问题关键是将条件和结论有机地结合起来,作适当变形,把握递推的规律.

练习册系列答案
相关题目
下列哪个函数与y=x是相同函数( )
A、y=
| |||
B、y=
| |||
C、y=
| |||
| D、y=alogax(a>0且a≠1) |
已知函数f(x)在x∈R上恒有f(-x)=f(x),若对于x≥0,都有f(x+2)=f(x),且当x∈[0,2)时,f(x)=log2(x+1),则f(-2014)+f(2015)的值为( )
| A、-2 | B、-1 | C、1 | D、2 |
已知从A口袋中摸出一个球是红球的概率为
,从B口袋中摸出一个球是红球的概率为
.现从两个口袋中各摸出一个球,那么这两个球中没有红球的概率是( )
| 1 |
| 3 |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
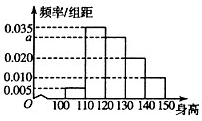 从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取20人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为
从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取20人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为