题目内容
若圆x2+y2-4x-4y-10=0上至少有三个不同的点到直线l：ax+by=0的距离为2
，则直线l的倾斜角的取值范围是（ ）
| 2 |
| A、[15°，60°] |
| B、[0°，90°] |
| C、[30°，60°] |
| D、[15°，75°] |
考点：直线的倾斜角
专题：直线与圆
分析：求出圆心和半径，比较半径和2
的大小，根据题意得出圆心到直线的距离小于等于
，求圆心到直线的距离公式，从而得直线斜率，即得倾斜角范围．
| 2 |
| 2 |
解答：
解：圆x2+y2-4x-4y-10=0可化为（x-2）2+（y-2）2=18，
∴圆心坐标为M（2，2），半径为r=
=3
，
所求的圆上至少有三个不同的点到直线l：ax+by=0的距离为2
，
∴圆心M到直线l的距离d应小于等于
，
即d=
≤
，
整理得(
)2+4（
）+1≤0，
解得-2-
≤
≤-2+
，
∴2-
≤-
≤2+
，
即直线l的斜率k=-
∈[2-
，2+
]，
即k=tnaα∈[2-
，2+
]，
∴直线l的倾斜角的取值范围是α∈[15°，75°]；
故选：D．
∴圆心坐标为M（2，2），半径为r=
| 18 |
| 2 |
所求的圆上至少有三个不同的点到直线l：ax+by=0的距离为2
| 2 |
∴圆心M到直线l的距离d应小于等于
| 2 |
即d=
| |2a+2b| | ||
|
| 2 |
整理得(
| a |
| b |
| a |
| b |
解得-2-
| 3 |
| a |
| b |
| 3 |
∴2-
| 3 |
| a |
| b |
| 3 |
即直线l的斜率k=-
| a |
| b |
| 3 |
| 3 |
即k=tnaα∈[2-
| 3 |
| 3 |
∴直线l的倾斜角的取值范围是α∈[15°，75°]；
故选：D．
点评：本题考查了直线和圆的位置关系以及圆心到直线的距离等知识，是易错题．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
若复数i满足z（1+i）=2i，则在复平面内z对应的点的坐标是（ ）
| A、（1，1） |
| B、（1，-1） |
| C、（-1，1） |
| D、（-1，-1） |
f（x）是定义域为R的奇函数，且当x≥0时，f（x）=x（x-2）；若关于x的方程f2（x）-f（x）+t=0的方程有6个不相等的实根，求实数t的取值范围（ ）
A、（0，
| ||
B、（-∞，
| ||
C、（-2，
| ||
| D、（-2，+∞） |
若A（-2，3）、B（3，-2）、C（
，m﹚三点在同一直线上，则m的值为（ ）
| 1 |
| 2 |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
不等式
≤
的解集是（ ）
| 1 |
| x |
| 1 |
| 2 |
| A、（2，+∞） |
| B、[2，+∞） |
| C、（-∞，0）∪[2，+∞） |
| D、（-∞，0]∪[2，+∞） |
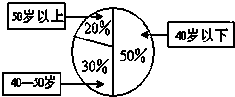某单位200名职工的年龄分布情况如图，现要从中抽取40名职工作样本，用系统抽样法，将全体职工随机按1-200编号，并按编号顺序平均分为40组（1-5号，6-10号，…，196-200号）．若第6组抽出的号码为28，则第8组抽出的号码应是a； 若用分层抽样方法，则50岁以下年龄段应抽取b人．那么a+b等于（ ）