题目内容
5.已知函数f(x)=ex+3,则f(x)在x=0处切线的方程是( )| A. | x-y+4=0 | B. | x+y-4=0 | C. | 4x-y+4=0 | D. | 4x+y-4=0 |
分析 求出函数的导数,求得切线的斜率和切点,由斜截式方程可得切线的方程.
解答 解:函数f(x)=ex+3的导数为f′(x)=ex,
即有f(x)在x=0处切线的斜率为k=e0=1,
切点为(0,4),
则f(x)在x=0处切线的方程为y=x+4,
故选:A.
点评 本题考查导数的运用:求切线方程,正确求导和运用直线方程的形式是解题的关键.

练习册系列答案
相关题目
13.若a,b∈R,且ab>0,则“a=b”是“$\frac{b}{a}+\frac{a}{b}≥2$等号成立”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既非充分又非必要条件 |
20.已知O为坐标原点,点A(-1,2),若点M(x,y)为平面区域$\left\{\begin{array}{l}{x+y≥2}\\{x≤1}\\{y≤2}\end{array}\right.$上的一个动点,则$\overrightarrow{OA}$•$\overrightarrow{OM}$的取值范围是( )
| A. | [-1,0] | B. | [0,1] | C. | [1,3] | D. | [1,4] |
17.已知圆x2+y2+2x+4y-4=0,若圆上恰有3个点到直线y=-x+b的距离为1,则b的值为( )
| A. | $3-2\sqrt{2}$ | B. | $-3+2\sqrt{2}$ | C. | $-3±2\sqrt{2}$ | D. | $3±2\sqrt{2}$ |
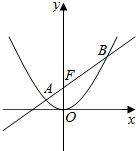 已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.
已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点. 如图,是一曲边三角形地块,其中曲边AB是以A为顶点,AC为对称轴的抛物线的一部分,点B到边AC的距离为2km,另外两边AC,BC的长度分别为8km,2$\sqrt{5}$km.现欲在此地块内建一形状为直角梯形DECF的科技园区.
如图,是一曲边三角形地块,其中曲边AB是以A为顶点,AC为对称轴的抛物线的一部分,点B到边AC的距离为2km,另外两边AC,BC的长度分别为8km,2$\sqrt{5}$km.现欲在此地块内建一形状为直角梯形DECF的科技园区.