题目内容
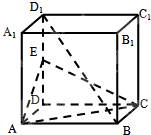如图，正方体ABCD-A1B1C1D1中，E是DD1的中点．（1）求证：BD1∥平面AEC．
（2）求异面直线BC1与AC所成的角．
考点：直线与平面平行的判定,异面直线及其所成的角
专题：空间位置关系与距离
分析：（1）利用线面平行的判定定理进行证明．
（2）连结AD1、CD1，可证出四边形ABC1D1是平行四边形，得BC1∥AD1，得∠D1AC（或补角）就是异面直线AC与BC1所成角．等边△AD1C中求出∠D1AC=60°，即得异面直线AC与BC1所成角的大小．
（2）连结AD1、CD1，可证出四边形ABC1D1是平行四边形，得BC1∥AD1，得∠D1AC（或补角）就是异面直线AC与BC1所成角．等边△AD1C中求出∠D1AC=60°，即得异面直线AC与BC1所成角的大小．
解答：
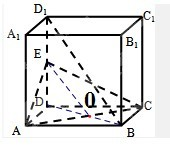解：（1）连结BD交AC于O，则O为BD的中点，
连EO，因为E是DD1的中点，所以EO∥BD1，
又EO?面AEC，BD1?面AEC，
所以BD1∥平面AEC．
（2）连结AD1、CD1，
∵正方体ABCD-A1B1C1D1中，AB
C1D1，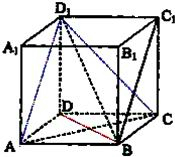
∴四边形ABC1D1是平行四边形，得BC1∥AD1，
由此可得∠D1AC（或补角）就是异面直线AC与BC1所成角．
∵△AD1C是等边三角形，
∴∠D1AC=60°，即异面直线AC与BC1所成角的大小为60°．
解：（1）连结BD交AC于O，则O为BD的中点，连EO，因为E是DD1的中点，所以EO∥BD1，
又EO?面AEC，BD1?面AEC，
所以BD1∥平面AEC．
（2）连结AD1、CD1，
∵正方体ABCD-A1B1C1D1中，AB
| ∥ |
. |
∴四边形ABC1D1是平行四边形，得BC1∥AD1，
由此可得∠D1AC（或补角）就是异面直线AC与BC1所成角．
∵△AD1C是等边三角形，
∴∠D1AC=60°，即异面直线AC与BC1所成角的大小为60°．
点评：本题在正方体中证明线面垂直，线面平行并求异面直线所成角的大小，着重考查了正方体的性质、线面垂直的判定与性质和异面直线所成角的定义与求法等知识，属于中档题．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
若函数f（x）=x3-bx，（b∈R）在区间（1，2）上有零点，则b的取值范围是（ ）
| A、（4，+∞） |
| B、（1，4） |
| C、（-4，-1） |
| D、（-∞，1） |