题目内容
复数z=
,若z2+
<0,求纯虚数a.
| (1+i)2+3(1-i) |
| 2+i |
| a |
| z |
考点:复数代数形式的混合运算,复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用复数的运算法则可得:复数z=1-i.设a=bi(b∈R),再利用复数的运算法则把z2+
<0,化为-
+(
-2)i<0,从而得到-
<0,
-2=0,解得b即可.
| a |
| z |
| b |
| 2 |
| b |
| 2 |
| b |
| 2 |
| b |
| 2 |
解答:
解:复数z=
=
=
=
=1-i.
设a=bi(b∈R),
∴z2+
=(1-i)2+
=-2i+
=-2i+
=-
+(
-2)i<0,
∴-
<0,
-2=0,解得b=4.
∴a=4i.
| (1+i)2+3(1-i) |
| 2+i |
| 2i+3-3i |
| 2+i |
| (3-i)(2-i) |
| (2+i)(2-i) |
| 5-5i |
| 5 |
设a=bi(b∈R),
∴z2+
| a |
| z |
| bi |
| 1-i |
| bi(1+i) |
| (1-i)(1+i) |
| -b+bi |
| 2 |
| b |
| 2 |
| b |
| 2 |
∴-
| b |
| 2 |
| b |
| 2 |
∴a=4i.
点评:本题考查了复数的运算法则、纯虚数的定义、复数为实数的充要条件,考查了计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知实数a和b,记f(a,b)=
,g(a,b)=
,那么下列结论中不能恒成立的是( )
| a+b+|a-b| |
| 2 |
| a+b-|a-b| |
| 2 |
| A、f(a,b)=f(b,a) |
| B、g(a,b)=g(b,a) |
| C、g(a,f(b,c))=f(g(a,b),g(b,c)) |
| D、f(a,f(b,c))=f(f(a,b),c) |
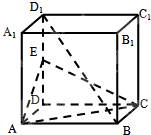 如图,正方体ABCD-A1B1C1D1中,E是DD1的中点.
如图,正方体ABCD-A1B1C1D1中,E是DD1的中点.