题目内容
设等比数列{an}的各项均为正数,公比为q,前n项和为Sn,若对任意n∈N+,有S2n<3Sn,则q的取值范围是 .
考点:等比数列的前n项和
专题:等差数列与等比数列
分析:验证当q=1时,S2n<3Sn成立,当q≠1时,由S2n<3Sn恒成立可得
<
,整理可求q的范围.
| a1(1-q2n) |
| 1-q |
| 3a1(1-qn) |
| 1-q |
解答:
解:当q=1时,S2n<3Sn成立,
当q≠1时,由S2n<3Sn恒成立,得
<
,
整理可得,qn<1恒成立,
∵q>0
∴0<q<1
综上可得0<q≤1.
故答案为:(0,1].
当q≠1时,由S2n<3Sn恒成立,得
| a1(1-q2n) |
| 1-q |
| 3a1(1-qn) |
| 1-q |
整理可得,qn<1恒成立,
∵q>0
∴0<q<1
综上可得0<q≤1.
故答案为:(0,1].
点评:本题主要考查了等比数列的求和公式的应用,解答的关键是对公比的讨论,是中档题.

练习册系列答案
相关题目
已知实数a和b,记f(a,b)=
,g(a,b)=
,那么下列结论中不能恒成立的是( )
| a+b+|a-b| |
| 2 |
| a+b-|a-b| |
| 2 |
| A、f(a,b)=f(b,a) |
| B、g(a,b)=g(b,a) |
| C、g(a,f(b,c))=f(g(a,b),g(b,c)) |
| D、f(a,f(b,c))=f(f(a,b),c) |
 如图,AB为圆O的直径,点E,F在圆O上,且AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E,F在圆O上,且AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直,且AB=2,AD=EF=1.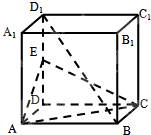 如图,正方体ABCD-A1B1C1D1中,E是DD1的中点.
如图,正方体ABCD-A1B1C1D1中,E是DD1的中点.