题目内容
在数列{an}中,a1=5,an+1=3an-4n+2,其中n∈N*.
(1)设bn=an-2n,证明数列{bn}是等比数列
(2)记数列{an}的前n项和为Sn,若对任意正整数n,Sn-(n2+241n)≥10m恒成立,求实数m的最大整数值.
(1)设bn=an-2n,证明数列{bn}是等比数列
(2)记数列{an}的前n项和为Sn,若对任意正整数n,Sn-(n2+241n)≥10m恒成立,求实数m的最大整数值.
考点:数列递推式,数列与不等式的综合
专题:综合题,等差数列与等比数列
分析:(1)由题意an+1=3an-4n+2,构造新的数列bn=an-2n,利用等比数列的定义即可以判断;
(2)因为数列{an}的前n项和为Sn且由(1)知道an=2n+3n 利用分组求和法求和Sn,Sn-(n2+241n)=
(3n-1)-240n=
(3n-160n)-
,所以,当n∈{1,2,3,4,5,6}时,f(n)≥f(6)=-231,当n∈N*且n≥7时,f(n)≥f(7)=1067,即可求实数m的最大整数值.
(2)因为数列{an}的前n项和为Sn且由(1)知道an=2n+3n 利用分组求和法求和Sn,Sn-(n2+241n)=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解答:
(1)证明:由an+1=3an-4n+2得an+1-2(n+1)=3(an-2n),
又b1=a1-2n=5-2×2=1≠0,bn=an-2n≠0,
所以,数列{bn}是首项为3,公比为3的等比数列,
(2)解:an-2n=3n⇒an=2n+3n,Sn=
(3n-1)+n(n+1),
Sn-(n2+241n)=
(3n-1)-240n=
(3n-160n)-
所以,当n∈{1,2,3,4,5,6}时,f(n)≥f(6)=-231,当n∈N*且n≥7时,f(n)≥f(7)=1067
因为对任意正整数n,Sn-(n2+241n)≥10m恒成立,
所以,-231≥10m,
所以实数m的最大整数值是-24.
又b1=a1-2n=5-2×2=1≠0,bn=an-2n≠0,
所以,数列{bn}是首项为3,公比为3的等比数列,
(2)解:an-2n=3n⇒an=2n+3n,Sn=
| 3 |
| 2 |
Sn-(n2+241n)=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
所以,当n∈{1,2,3,4,5,6}时,f(n)≥f(6)=-231,当n∈N*且n≥7时,f(n)≥f(7)=1067
因为对任意正整数n,Sn-(n2+241n)≥10m恒成立,
所以,-231≥10m,
所以实数m的最大整数值是-24.
点评:此题考查了已知数列的前n项的和,求出通项,还考查了分组求和法求和,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 是
是 上的减函数,则
上的减函数,则 的取值范围是( )
的取值范围是( ) C.
C.  D.
D. 
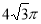 ,则该正方体的
,则该正方体的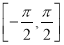 上随机取一个
上随机取一个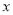 ,
,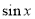 的值介于
的值介于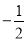 与
与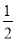 之间的概率为( )
之间的概率为( )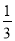 (B)
(B) (C)
(C) (D)
(D)
 如图,AB为圆O的直径,点E,F在圆O上,且AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E,F在圆O上,且AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直,且AB=2,AD=EF=1. 如图,正方体ABCD-A1B1C1D1中,E、F分别是CD、CC1的中点.证明:EF∥平面AB1D1.
如图,正方体ABCD-A1B1C1D1中,E、F分别是CD、CC1的中点.证明:EF∥平面AB1D1.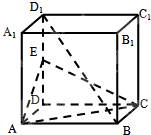 如图,正方体ABCD-A1B1C1D1中,E是DD1的中点.
如图,正方体ABCD-A1B1C1D1中,E是DD1的中点.