题目内容
若函数f(x)=x3-bx,(b∈R)在区间(1,2)上有零点,则b的取值范围是( )
| A、(4,+∞) |
| B、(1,4) |
| C、(-4,-1) |
| D、(-∞,1) |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:由根的存在性定理,令f(1)•f(2)<0,解不等式,求出b的取值范围.
解答:
解:∵函数f(x)=x3-bx在区间(1,2)上有零点,
∴f(1)•f(2)<0,
即(1-b)(8-2b)<0;
∴(b-1)(b-4)<0,
解得1<b<4,
∴b的取值范围是(1,4).
故选:B.
∴f(1)•f(2)<0,
即(1-b)(8-2b)<0;
∴(b-1)(b-4)<0,
解得1<b<4,
∴b的取值范围是(1,4).
故选:B.
点评:本题考查了函数零点的应用问题,解题的关键是由根的存在性定理列出不等式,是基础题目.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
已知实数a和b,记f(a,b)=
,g(a,b)=
,那么下列结论中不能恒成立的是( )
| a+b+|a-b| |
| 2 |
| a+b-|a-b| |
| 2 |
| A、f(a,b)=f(b,a) |
| B、g(a,b)=g(b,a) |
| C、g(a,f(b,c))=f(g(a,b),g(b,c)) |
| D、f(a,f(b,c))=f(f(a,b),c) |
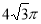 ,则该正方体的
,则该正方体的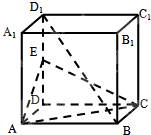 如图,正方体ABCD-A1B1C1D1中,E是DD1的中点.
如图,正方体ABCD-A1B1C1D1中,E是DD1的中点.