题目内容
19.已知顶点在原点,对称轴为y轴的抛物线C过点(2,-2).(1)求抛物线C的方程;
(2)若抛物线C与过点P(0,-1)的直线l相交于A,B两点,O为坐标原点,若直线OA和OB的斜率之和为2,求直线l的方程.
分析 (1)由题意,可设抛物线方程为x2=-2py,点(2,-2)代入方程可得4=4p,即可求抛物线C的方程;
(2)由题意可得设直线l的方程为y=kx-1,联立直线与抛物线的方程可得:x2+2kx-2=0,根据韦达定理可得答案.
解答 解:(1)由题意,可设抛物线方程为x2=-2py,
将点(2,-2)代入方程可得4=4p,即p=1…(2分)
所以抛物线的方程为x2=-2y.…(4分)
(2)显然,直线l垂直于x轴不合题意,故可设所求的直线方程为y=kx-1,
代入抛物线方程化简,得:x2+2kx-2=0,…(6分)
其中△=4k2+8>0,x1+x2=-2k,x1x2-2…(8分)
设点A(x1,y1),B(x2,y2),则有$\frac{y_1}{x_1}+\frac{y_2}{x_2}=2$,①
因为y1=kx1-1,y2=kx2-1,代入①,整理可得$2k-\frac{{{x_1}+{x_2}}}{{{x_1}{x_2}}}=2$,
将x1+x2=-2k,x1x2-2代入,可得k=2,…(11分)
所以直线l的方程为y=2x-1.…(12分)
点评 本题主要考查抛物线的简单性质、直线的一般式方程、直线与抛物线的位置关系,以及方程思想,属于中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
9.执行如图所示的程序框图,如果输入的t∈[-1,2],则输出的s属于( )
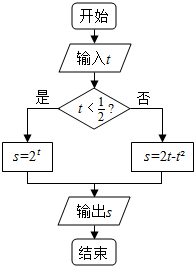

| A. | [0,1] | B. | [$\frac{3}{4}$,$\sqrt{2}$] | C. | [0,$\sqrt{2}$] | D. | [1,$\sqrt{2}$) |
4.下列各式中正确的是( )
| A. | -$\sqrt{x}$=(-x)${\;}^{\frac{1}{2}}$ | B. | x${\;}^{-\frac{1}{5}}$=-$\root{5}{x}$ | C. | (-x)${\;}^{\frac{2}{3}}$=x${\;}^{\frac{2}{3}}$ | D. | x${\;}^{\frac{2}{6}}$=x${\;}^{\frac{1}{3}}$ |
11.设$\frac{π}{2}$<α<π,若sin(α+$\frac{π}{6}$)=$\frac{1}{3}$,则cos($\frac{2π}{3}$+α)=( )
| A. | -$\frac{2\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
9.已知四面体ABCD,$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,$\overrightarrow{DC}$=$\overrightarrow{c}$,点M在棱DA上,$\overrightarrow{DM}$=2$\overrightarrow{MA}$,N为BC中点,则$\overrightarrow{MN}$=( )
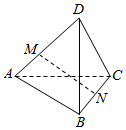

| A. | -$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ | B. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
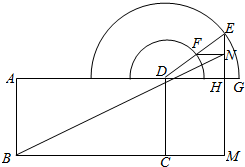 如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.
如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.