题目内容
17.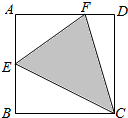 如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在△CEF内的概率为( )
如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在△CEF内的概率为( )| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{7}{12}$ | D. | $\frac{5}{12}$ |
分析 设正方形ABCD的边长为a,求出正方形ABCD的面积与△AEF、△BEC和△CDF的面积,即可得出△CEF的面积,从而求出对应的概率.
解答 解:设正方形ABCD的边长为a,
则正方形ABCD的面积为a2,
又△AEF的面积为S△AEF=$\frac{1}{2}$×$\frac{1}{2}$a•$\frac{2}{3}$a=$\frac{1}{6}$a2,
△BEC的面积为S△BEC=$\frac{1}{2}$×$\frac{1}{2}$a•a=$\frac{1}{4}$a2,
△CDF的面积为S△CDF=$\frac{1}{2}$×$\frac{1}{3}$a•a=$\frac{1}{6}$a2,
∴△CEF的面积为S△CEF=a2-$\frac{1}{6}$a2-$\frac{1}{6}$a2-$\frac{1}{4}$a2=$\frac{5}{12}$a2;
∴向正方形ABCD内随机投掷一个质点,它落在△CEF内的概率为P=$\frac{5}{12}$.
故选:D.
点评 本题考查了几何概型的概率计算问题,几何概型中的“几何度量”,可以为线段长度、面积、体积等,而且“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.在四面体ABCD中,E、G分别是CD、BE的中点,若$\overrightarrow{AG}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{AC}$,则x+y+z=( )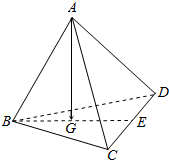

| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
9.已知四面体ABCD,$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,$\overrightarrow{DC}$=$\overrightarrow{c}$,点M在棱DA上,$\overrightarrow{DM}$=2$\overrightarrow{MA}$,N为BC中点,则$\overrightarrow{MN}$=( )
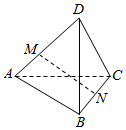

| A. | -$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ | B. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
7.已知[t]表示不超过t的最大整数,例如[1.25]=1,[2]=2,若关于x的方程$\frac{[x]}{x-1}$=a在(1,+∞)恰有2个不同的实数解,则实数a的取值范围是( )
| A. | [2,+∞) | B. | (2,+∞) | C. | ($\frac{3}{2}$,2] | D. | [$\frac{3}{2}$,2] |
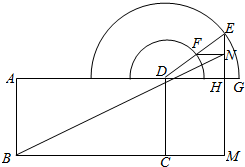 如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.
如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.