题目内容
13.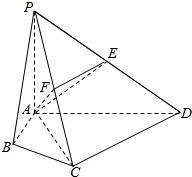 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2. (1)求四棱锥P-ABCD的体积V;
(2)若F为PC的中点,求证PC⊥平面AEF.
分析 (1)利用直角三角形的边角关系可得BC,CD.SABCD=$\frac{1}{2}AB•BC+\frac{1}{2}AC•CD$,利用V=$\frac{1}{3}$S四边形ABCD×PA,即可得出.
(2)在Rt△ABC,∠BAC=60°,可得AC=2AB,PA=CA,又F为PC的中点,可得AF⊥PC.利用线面垂直的判定与性质定理可得:CD⊥PC.利用三角形的中位线定理可得:EF∥CD.于是EF⊥PC.即可证明PC⊥平面AEF.
解答 (本题满分12分)
解:(1)∵在Rt△ABC中,AB=1,∠BAC=60°,
∴BC=$\sqrt{3}$,AC=2.
在Rt△ACD中,AC=2,∠CAD=60°,
∴CD=2$\sqrt{3}$,AD=4.
∴SABCD=$\frac{1}{2}AB•BC+\frac{1}{2}AC•CD$=$\frac{1}{2}×1×\sqrt{3}+\frac{1}{2}×2×2\sqrt{3}=\frac{5}{2}\sqrt{3}$.
则V=$\frac{1}{3}×\frac{5}{2}\sqrt{3}×2=\frac{5}{3}\sqrt{3}$.….(6分)
(2)∵PA=CA,F为PC的中点,
∴AF⊥PC.
∵PA⊥平面ABCD,
∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,
∴CD⊥平面PAC.
∴CD⊥PC.
∵E为PD中点,F为PC中点,
∴EF∥CD.则EF⊥PC.
∵AF∩EF=F,
∴PC⊥平面AEF. …(12分)
点评 本题考查了线面垂直的判定与性质定理、三角形的中位线定理、直角三角形的边角关系、四棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
4.下列各式中正确的是( )
| A. | -$\sqrt{x}$=(-x)${\;}^{\frac{1}{2}}$ | B. | x${\;}^{-\frac{1}{5}}$=-$\root{5}{x}$ | C. | (-x)${\;}^{\frac{2}{3}}$=x${\;}^{\frac{2}{3}}$ | D. | x${\;}^{\frac{2}{6}}$=x${\;}^{\frac{1}{3}}$ |
1.函数f(x)=$\frac{lg(x+2)}{x-1}$的定义域是( )
| A. | (-2,1) | B. | [-2,1)∪(1,+∞) | C. | (-2,+∞) | D. | (-2,1)∪(1,+∞) |
18.甲乙两人下棋,甲获胜的概率为30%,甲不输的概率为80%,则甲乙下成和棋的概率为( )
| A. | 70% | B. | 30% | C. | 20% | D. | 50% |
3.已知圆锥的母线长是10,侧面展开图是半圆,则该圆锥的侧面积为( )
| A. | $\frac{100}{3}$π | B. | 100π | C. | $\frac{50}{3}$π | D. | 50π |