题目内容
已知三个数2,m,8构成一个等比数列,则圆锥曲线
+
=1离心率为 .
| x2 |
| m |
| y2 |
| 2 |
考点:双曲线的简单性质,椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由1,m,9构成一个等比数列,得到m=±3.当m=3时,圆锥曲线是椭圆;当m=-3时,圆锥曲线是双曲线,由此入手能求出离心率.
解答:
解:∵2,m,8构成一个等比数列,
∴m=±4.
当m=4时,圆锥曲线
+
=1是椭圆,它的离心率是
;
当m=-4时,圆锥曲线
+
=1是双曲线,它的离心率是
.
故答案为:
或
.
∴m=±4.
当m=4时,圆锥曲线
| x2 |
| m |
| y2 |
| 2 |
| ||
| 2 |
当m=-4时,圆锥曲线
| x2 |
| m |
| y2 |
| 2 |
| 3 |
故答案为:
| ||
| 2 |
| 3 |
点评:本题考查圆锥曲线的离心率的求法,解题时要注意等比数列的性质的合理运用,注意分类讨论思想的灵活运用.

练习册系列答案
相关题目
如图,直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分,求k的值( )


A、1-
| |||||
B、1-
| |||||
C、1-
| |||||
D、1-
|
命题p:?x∈R,ax2+ax+1≥0,若?p是真命题,则实数a的取值范围是( )
| A、(0,4] |
| B、[0,4] |
| C、(-∞,0]∪[4,+∞) |
| D、(-∞,0)∪(4,+∞) |
已知函数f(x),g(x)分别由表给出:
则满足f(g(x))<g(f(x))的x的值为( )
| x | 1 | 2 | 3 |
| f(x) | 1 | 1 | 1 |
| x | 1 | 2 | 3 |
| g(x) | 3 | 2 | 1 |
| A、1 | B、2 |
| C、1或2 | D、1或2或3 |
已知a≤
,x∈(-∞,a],则函数f(x)=x2-x+a+1的值域是( )
| 1 |
| 2 |
A、[a+
| ||
| B、[a2+1,+∞) | ||
| C、[1,+∞) | ||
D、[
|
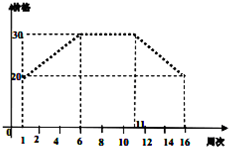 在某服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元/件(第一周价格),并且每周价格上涨,如图所示,从第6周开始到第11轴保持30元/件的价格平稳销售;从第12周开始,当季节即将过去时,每周下跌,直到第16周周末,该服装不再销售.
在某服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元/件(第一周价格),并且每周价格上涨,如图所示,从第6周开始到第11轴保持30元/件的价格平稳销售;从第12周开始,当季节即将过去时,每周下跌,直到第16周周末,该服装不再销售.