题目内容
已知集合A={x|
≤0}，B={x|1＜x＜a}，（其中a＞1）．
（1）若a=10，求A∪B，（∁RA）∩B；
（2）若A∩B≠∅，求a的取值范围．
| x-3 |
| x-7 |
（1）若a=10，求A∪B，（∁RA）∩B；
（2）若A∩B≠∅，求a的取值范围．
考点：交、并、补集的混合运算
专题：集合
分析：（1）首先化简集合A，计算∁RA，然后求集合的运算；
（2）利用A∩B≠∅，得到端点a与3关系结合已知解答．
（2）利用A∩B≠∅，得到端点a与3关系结合已知解答．
解答：
解：由已知，A={x|3≤x＜7}，
（1）a=10时，B={x|1＜x＜10}，∁RA={x|x＜3或x≥7}，
所以A∪B=B={x|1＜x＜10}，（∁RA）∩B={x|1＜x＜3或7≤x＜10}；
（2）因为A∩B≠∅，所以只要a＞3，又有a＞1，所以a＞3．
（1）a=10时，B={x|1＜x＜10}，∁RA={x|x＜3或x≥7}，
所以A∪B=B={x|1＜x＜10}，（∁RA）∩B={x|1＜x＜3或7≤x＜10}；
（2）因为A∩B≠∅，所以只要a＞3，又有a＞1，所以a＞3．
点评：本题考查了集合的化简与运算，数集的运算结合数轴直观运算较好．
练习册系列答案
相关题目
由于被墨水污染，一道数学题仅能见到如下文字：已知二次函数y=x2+bx+c的图象经过（1，0），…，求证：这个二次函数的图象关于直线x=2对称．根据已知信息，题中二次函数图象不具有的性质是（ ）
| A、过点（3，0） |
| B、顶点（2，-2） |
| C、在x轴上截线段长是2 |
| D、与y轴交点是（0，3） |
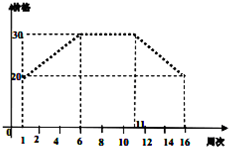在某服装批发市场，某种品牌的时装当季节将来临时，价格呈上升趋势，设这种时装开始时定价为20元/件（第一周价格），并且每周价格上涨，如图所示，从第6周开始到第11轴保持30元/件的价格平稳销售；从第12周开始，当季节即将过去时，每周下跌，直到第16周周末，该服装不再销售．集合A={x|
≥0}B={x||x-1|＜3}，则A∩B=（ ）
| x-1 |
| x+1 |
| A、（-2，-1） |
| B、[1，4） |
| C、（-2，-1）∪[1，4） |
| D、（-2，4） |
已知函数f（x），g（x）分别由表给出：
则满足f（g（x））＜g（f（x））的x的值为（ ）
| x | 1 | 2 | 3 |
| f（x） | 1 | 1 | 1 |
| x | 1 | 2 | 3 |
| g（x） | 3 | 2 | 1 |
| A、1 | B、2 |
| C、1或2 | D、1或2或3 |