题目内容

18．已知点P（t，t-1），t∈R，点E是圆x2+y2=$\frac{1}{4}$上的动点，点F是圆（x-3）2+（y+1）2=$\frac{9}{4}$上的动点，则|PF|-|PE|的最大值为（　　）
A．2B．$\frac{5}{2}$C．3D．4

分析 由题意，P在直线y=x-1上运动，E（0，0）关于直线的对称点的坐标为A（1，-1），由此可得|PF|-|PE|的最大值．

解答 解：由题意，P在直线y=x-1上运动，E（0，0）关于直线的对称点的坐标为A（1，-1），
∵F（3，-1），
∴|PF|-|PE|的最大值为|AF|=4，
故选D．

点评 本题考查圆与圆的位置关系，直线与圆的位置关系，考查点关于直线对称点的求法，属于中档题．

练习册系列答案
相关题目
17．函数y=f（x）导函数的图象如图所示，则下列说法错误的是（　　）
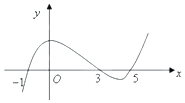
A．（-1，3）为函数y=f（x）的递增区间B．（3，5）为函数y=f（x）的递减区间
C．函数y=f（x）在x=0处取得极大值D．函数y=f（x）在x=5处取得极小值
9．“m＞n＞0”是方程mx2+ny2=1表示椭圆的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
6．已知P（0，-1）是椭圆C的下顶点，F是椭圆C的右焦点，直线PF与椭圆C的另一个交点为Q，满足$\overrightarrow{PF}$=7$\overrightarrow{FQ}$．
（1）求椭圆C的标准方程；
（2）如图，过左顶点A作斜率为k（k＞0）的直线l1，l2，直线l1交椭圆C于点D，交y轴于点B．l2与椭圆C的一个交点为E，求$\frac{|AD|+|AB|}{|OE|}$的最小值．
13．如果实数x，y满足（x-2）2+y2=2，则$\frac{y}{x}$的范围是（　　）
A．（-1，1）B．[-1，1]C．（-∞，-1）∪（1，+∞）D．（-∞，-1]∪[1，+∞）
3．在平面直角坐标系中，△ABC三个顶点分别为A（2，4），B（1，-3），C（-2，1）．
（1）求BC边上的高所在的直线方程；
（2）设AC中点为D，求△DBC的面积．
10．设函数f（x）=$\frac{1}{2}$mx2-2x+ln（x+1）（m∈R）．
（Ⅰ）判断x=1能否为函数f（x）的极值点，并说明理由；
（Ⅱ）若存在m∈[-4，-1），使得定义在[1，t]上的函数g（x）=f（x）-ln（x+1）+x3在x=1处取得最大值，求实数t取值范围．
7．在△ABC中，$∠ABC=\frac{2π}{3}$，过B点作BD⊥AB交AC于点D．若AB=CD=1，则AD=$\root{3}{2}$．
8．在△ABC中，若b=3，A=120°，三角形的面积$S=\frac{9}{4}\sqrt{3}$，则三角形外接圆的半径为（　　）
A．$\frac{2}{3}\sqrt{3}$B．3C．$\frac{4}{3}\sqrt{3}$D．6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网