题目内容
2．若$tanθ=-\frac{1}{3}，θ∈（\frac{π}{2}，π），则cos2θ$=（ ）| A． | $-\frac{4}{5}$ | B． | -$\frac{1}{5}$ | C． | $\frac{1}{5}$ | D． | $\frac{4}{5}$ |
分析 利用二倍角公式，同角三角函数基本关系式化简所求，结合已知即可计算得解．
解答 解：∵tan$θ=-\frac{1}{3}$，
∴cos2θ=$\frac{co{s}^{2}θ-si{n}^{2}θ}{co{s}^{2}θ+si{n}^{2}θ}$=$\frac{1-ta{n}^{2}θ}{1+ta{n}^{2}θ}$=$\frac{1-\frac{1}{9}}{1+\frac{1}{9}}$=$\frac{4}{5}$．
故选：D．
点评 本题考查二倍角的余弦公式，考查同角三角函数关系的运用，比较基础．
练习册系列答案
中考解读考点精练系列答案
相关题目
12．已知m∈R，“方程ex+m-1=0有解”是“函数y=logmx在区间（0，+∞）为减函数”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
13．如果实数x，y满足（x-2）2+y2=2，则$\frac{y}{x}$的范围是（ ）
| A． | （-1，1） | B． | [-1，1] | C． | （-∞，-1）∪（1，+∞） | D． | （-∞，-1]∪[1，+∞） |
14．不等式2x2-x＞0的解集是（ ）
| A． | （-∞，0）∪（$\frac{1}{2}$，+∞） | B． | （-∞，$\frac{1}{2}$） | C． | （0，$\frac{1}{2}$） | D． | （$\frac{1}{2}$，+∞） |
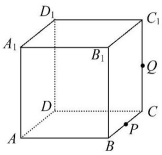如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S．则下列命题正确的是①②④（写出所有正确命题的编号）．