题目内容
已知数列{an}前n项的和为Sn，a1=1，an+an+1=2n-1，则S49= ．
考点：数列的求和
专题：点列、递归数列与数学归纳法
分析：根据数列关系得到an+2-an=2，利用等差数列的求和公式即可得到结论．
解答：
解：∵a1=1，an+an+1=2n-1，
∴an+1+an+2=2n+1，
两式相减an+2-an=2，即数列{an}的奇数项和偶数项，分别为等差数列，公差d=2，
∵a1=1，
∴a1+a2=2-1=1，即a2=0，
则S49=（a1+a3+…+a49）+（a2+a4+…+a48）=25a1+
×2+24a2+
×2=25+600+552=1177，
故答案为：1177；
∴an+1+an+2=2n+1，
两式相减an+2-an=2，即数列{an}的奇数项和偶数项，分别为等差数列，公差d=2，
∵a1=1，
∴a1+a2=2-1=1，即a2=0，
则S49=（a1+a3+…+a49）+（a2+a4+…+a48）=25a1+
| 25×24 |
| 2 |
| 24×23 |
| 2 |
故答案为：1177；
点评：本题主要考查数列的和的计算，利用条件得到an+2-an=2是解决本题的关键，考查等差数列的求和的应用．
练习册系列答案
相关题目
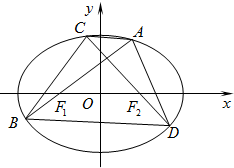已知椭圆