题目内容
已知平面上三个向量
,
,
,满足|
|=1,|
|=
,|
|=2,
•
=0,则
•
最大值是 .
| OA |
| OB |
| OC |
| OA |
| OB |
| 3 |
| OC |
| OA |
| OB |
| CA |
| CB |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由于满足|
|=1,|
|=
,|
|=2,
•
=0,建立如图所示的直角坐标系,可得A(1,0),B(0,
),可设C(2cosθ,2sinθ),θ∈[0,2π).再利用向量的坐标运算、数量积运算、两角和差的正弦公式、正弦函数的单调性有界性即可得出.
| OA |
| OB |
| 3 |
| OC |
| OA |
| OB |
| 3 |
解答:
解:∵满足|
|=1,|
|=
,|
|=2,
•
=0,
如图所示,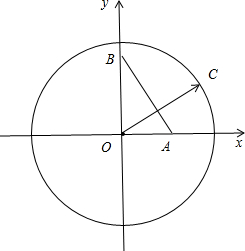
∴A(1,0),B(0,
),
可设C(2cosθ,2sinθ),θ∈[0,2π).
∴
=(1-2cosθ,-2sinθ),
=(-2cosθ,
-2sinθ),
∴
•
=-2cosθ(1-2cosθ)-2sinθ(
-2sinθ)
=-2cosθ-2
sinθ+4
=-4(
cosθ+
sinθ)+4
=-4sin(θ+
)+4≤8,当且仅当θ=
时取等号.
∴
•
最大值是8.
故答案为:8.
| OA |
| OB |
| 3 |
| OC |
| OA |
| OB |
如图所示,

∴A(1,0),B(0,
| 3 |
可设C(2cosθ,2sinθ),θ∈[0,2π).
∴
| CA |
| CB |
| 3 |
∴
| CA |
| CB |
| 3 |
=-2cosθ-2
| 3 |
=-4(
| 1 |
| 2 |
| ||
| 2 |
=-4sin(θ+
| π |
| 6 |
| 4π |
| 3 |
∴
| CA |
| CB |
故答案为:8.
点评:本题考查了向量的坐标运算、数量积运算、两角和差的正弦公式、正弦函数的单调性有界性,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图所示的三视图的几何体的体积为( )


A、
| ||
| B、1 | ||
| C、2 | ||
D、
|
确定结论“X与Y有关系”的可信度为99.5%时,则随即变量k2的观测值k必须( )
| A、小于7.879 |
| B、大于10.828 |
| C、小于6.635 |
| D、大于2.706 |
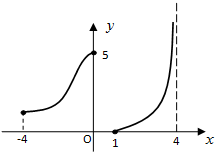 如图所示是函数y=f(x)的图象,图中曲线与直线无限接近但是永不相交,则以下描述正确的是( )
如图所示是函数y=f(x)的图象,图中曲线与直线无限接近但是永不相交,则以下描述正确的是( )| A、函数f(x)的定义域为[-4,4) |
| B、函数f(x)的值域为[0,5] |
| C、此函数在定义域中不单调 |
| D、对于任意的y∈[0,+∞),都有唯一的自变量x与之对应 |
