题目内容
如果函数f(x)=ax2+2x-3
(1)当a=1时,求f(x)在[-2,2]之间的取值范围.
(2)若f(x)在区间(-∞,4)上单调递增,求实数a的取值范围.
(1)当a=1时,求f(x)在[-2,2]之间的取值范围.
(2)若f(x)在区间(-∞,4)上单调递增,求实数a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)当a=1时,判断函数的对称轴,然后求f(x)在[-2,2]之间的取值范围.
(2)若f(x)在区间(-∞,4)上单调递增,分类讨论函数是一次函数还是二次函数,二次函数的对称轴与区间端点的关系,从而求实数a的取值范围.
(2)若f(x)在区间(-∞,4)上单调递增,分类讨论函数是一次函数还是二次函数,二次函数的对称轴与区间端点的关系,从而求实数a的取值范围.
解答:
解:(1)当a=1时,f(x)=x2+2x-3,
函数的对称轴为x=-1,
∴f(-1)=-4,f(2)=5.
函数在[-2,2]之间的取值范围:[-4,5].
(2)当a=0时,函数是f(x)=2x-3,f(x)在区间(-∞,4)上单调递增,恒成立;
当a≠0时,函数是二次函数,f(x)在区间(-∞,4)上单调递增,
∴a<0,
函数的对称轴x=-
,
则-
≥4解得-
≤a<0,
∴实数a的取值范围[-
,0].
函数的对称轴为x=-1,
∴f(-1)=-4,f(2)=5.
函数在[-2,2]之间的取值范围:[-4,5].
(2)当a=0时,函数是f(x)=2x-3,f(x)在区间(-∞,4)上单调递增,恒成立;
当a≠0时,函数是二次函数,f(x)在区间(-∞,4)上单调递增,
∴a<0,
函数的对称轴x=-
| 1 |
| a |
则-
| 1 |
| a |
| 1 |
| 4 |
∴实数a的取值范围[-
| 1 |
| 4 |
点评:本题主要考查了函数单调性的应用及分类讨论的思想,解题的关键是比较区间端点与二次函数的对称轴,但是不要漏掉对一次函数即a=0时的考虑.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
 空气质量已成为城市居住环境的一项重要指标,空气质量的好坏由空气质量指数确定.空气质量指数越高,代表空气污染越严重:
空气质量已成为城市居住环境的一项重要指标,空气质量的好坏由空气质量指数确定.空气质量指数越高,代表空气污染越严重: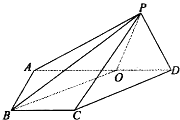 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.