题目内容

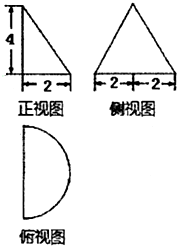
一个几何体的三视图如图所示，则这个几何体的体积是（　　）
A、
2π
3
B、
4π
3
C、
8π
3
D、
16π
3
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：几何体为半圆锥，根据三视图判断半圆锥的底面半径与高，把数据代入半圆锥的体积公式计算．
解答： 解：由三视图知：几何体为半圆锥，且半圆锥的底面半径为2，高为4，
∴半圆锥的体积V=
1
2
×
1
3
×π×22×4=
8π
3
．
故选：C．
点评：本题考查了由三视图求几何体的体积，判断三视图的数据所对应的几何量是关键．
练习册系列答案
相关题目
已知全集U={x|x＞0}，集合M={x|2x-x2＞0}，则∁UM=（　　）
A、{x|x≥2}
B、{x|x＞2}
C、{x|x≤0或x≥2}
D、{x|0＜x＜2}
将函数f（x）=sin（2x+φ）（0＜φ＜π）的图象上所有点向右平移
π
6
个单位后得到的图象关于原点对称，则φ等于（　　）
A、0
B、
π
6
C、
π
3
D、
π
2
动曲线Γ1的初始位置所对应的方程为：
x2
a2
-
y2
b2
=1（x＜0），一个焦点为F1（-c，0），曲线Γ2：
x2
a2
-
y2
b2
=1（x＞0）的一个焦点为F2（c，0），其中a＞0，b＞0，c=
a2+b2
．现将Γ1沿x轴向右平行移动．给出以下三个命题：
①Γ2的两条渐近线与Γ1的交点个数可能有3个；
②当Γ2的两条渐近线与Γ1的交点及Γ2的顶点在同一直线上时，曲线Γ1平移了（
2
+1）a个单位长度；
③当F1与F2重合时，若Γ1，Γ2的公共弦长恰为两顶点距离的4倍，则Γ1的离心率为3．
其中正确的是（　　）
A、②③B、①②③C、①③D、②
等比数列{an}是递减数列，其前n项积为Tn，若T12=4T8，则a8•a13=（　　）
A、±1B、±2C、1D、2
一个空间几何体的三视图如图所示，该几何体的表面积为（　　）
A、96B、136
C、152D、192
程序框图（如图）的运算结果为（　　）
A、2B、6C、18D、24
已知a＞0且a≠1，则在下面所给出的四种图形中，正确表示函数y=ax和y=logax的图象一定是（　　）
A、①③B、②③C、②④D、①④
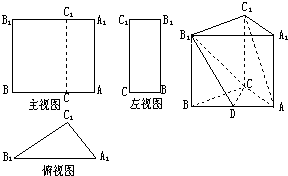已知三棱柱ABC-A1B1C1的三视图与直观图如图所示，其中主视图AA1B1B和左视图B1BCC1均为矩形，在俯视图△A1B1C1中，A1C1=3，A1B1=5，B1C1=4，
（1）在三棱柱ABC-A1B1C1中，求证：BC⊥AC1；
（2）若三棱柱的高为5，求三视图中左视图的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网