题目内容
等比数列{an}是递减数列，其前n项积为Tn，若T12=4T8，则a8•a13=（ ）
| A、±1 | B、±2 | C、1 | D、2 |
考点：等比数列的性质
专题：等差数列与等比数列
分析：直接由T12=4T8得a9a10a11a12=4，再由等比数列的性质结合数列{an}是递减数列得到a8•a13=2．
解答：
解：在等比数列{an}中，由T12=4T8，得：
a9a10a11a12=4，
∴a8a13=a9a12=±2．
∵数列{an}是递减数列，
∴a8•a13=2．
故选：D．
a9a10a11a12=4，
∴a8a13=a9a12=±2．
∵数列{an}是递减数列，
∴a8•a13=2．
故选：D．
点评：本题考查了等比数列的性质，在等比数列{an}中，若m，n，p，q∈N*，且m+n=p+q，则aman=apaq，是基础题．
练习册系列答案
相关题目
总体容量为203，若采用系统抽样法进行抽样，当抽样间距为多少时不需要剔除个体（ ）
| A、4 | B、5 | C、6 | D、7 |
在△ABC中，a=2
，b=2
，B=60°，则A等于（ ）
| 2 |
| 3 |
| A、30° |
| B、45° |
| C、30°或150° |
| D、45°或135° |
cos17°sin43°+sin163°sin47°（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
一个几何体的三视图如图所示，则这个几何体的体积是（ ）
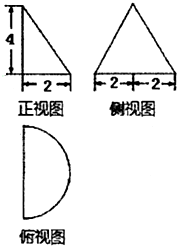
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f（x）（x∈R）是偶函数，函数g（x）（x∈R）是奇函数，则（ ）
| A、函数f[g（x）]是奇函数 |
| B、函数g[f（x）]是奇函数 |
| C、函数f（x）+g（x）是奇函数 |
| D、函数f（x）g（x）是奇函数 |
把88化为五进制数是（ ）
| A、233（5） |
| B、324（5） |
| C、323（5） |
| D、332（5） |