题目内容
动曲线Γ1的初始位置所对应的方程为:
-
=1(x<0),一个焦点为F1(-c,0),曲线Γ2:
-
=1(x>0)的一个焦点为F2(c,0),其中a>0,b>0,c=
.现将Γ1沿x轴向右平行移动.给出以下三个命题:
①Γ2的两条渐近线与Γ1的交点个数可能有3个;
②当Γ2的两条渐近线与Γ1的交点及Γ2的顶点在同一直线上时,曲线Γ1平移了(
+1)a个单位长度;
③当F1与F2重合时,若Γ1,Γ2的公共弦长恰为两顶点距离的4倍,则Γ1的离心率为3.
其中正确的是( )
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| a2+b2 |
①Γ2的两条渐近线与Γ1的交点个数可能有3个;
②当Γ2的两条渐近线与Γ1的交点及Γ2的顶点在同一直线上时,曲线Γ1平移了(
| 2 |
③当F1与F2重合时,若Γ1,Γ2的公共弦长恰为两顶点距离的4倍,则Γ1的离心率为3.
其中正确的是( )
| A、②③ | B、①②③ | C、①③ | D、② |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:①由已知条件知,Γ1沿x轴向右平行移动a个单位时,Γ2的两条渐近线与Γ1的交点个数为1个,由此利用由椭圆的对称性知Γ2的两条渐近线与Γ1的交点个数不可能有3个;②解方程组
,得Γ1的移动后的图象过点(a,b),(a,-b).把y=b代入:
-
=1(x<0),得x=-
a,由此求出曲线Γ1平移了(
+1)a个单位长度;③F1与F2重合时,Γ1,Γ2的公共弦长为
,由此能求出Γ1的离心率为e=
=
.
|
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
| 2b2 |
| a |
| c |
| a |
| 5 |
解答:
解:①由已知条件知,Γ1沿x轴向右平行移动a个单位时,
得到
-
=1,
联立方程组
,解得x=y=0,
∴由椭圆的对称性知Γ2的两条渐近线与Γ1的交点个数不可能有3个,故①错误;
②∵Γ2的两条渐近线与Γ1的交点及Γ2的顶点在同一直线上,
∴解方程组
,得Γ1的移动后的图象过点(a,b),(a,-b).
把y=b代入:
-
=1(x<0),得x=-
a,
∴曲线Γ1平移了(
+1)a个单位长度,故②正确;
③F1与F2重合时,解方程组
,
得Γ1,Γ2的公共弦长为
,
∵Γ1,Γ2的公共弦长恰为两顶点距离的4倍,
∴
=8a,解得b2=4a2,从而c2=5a2,
∴Γ1的离心率为e=
=
.故③不正确.
故选:D.
得到
| (x-a)2 |
| a2 |
| y2 |
| b2 |
联立方程组
|
∴由椭圆的对称性知Γ2的两条渐近线与Γ1的交点个数不可能有3个,故①错误;
②∵Γ2的两条渐近线与Γ1的交点及Γ2的顶点在同一直线上,
∴解方程组
|
把y=b代入:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
∴曲线Γ1平移了(
| 2 |
③F1与F2重合时,解方程组
|
得Γ1,Γ2的公共弦长为
| 2b2 |
| a |
∵Γ1,Γ2的公共弦长恰为两顶点距离的4倍,
∴
| 2b2 |
| a |
∴Γ1的离心率为e=
| c |
| a |
| 5 |
故选:D.
点评:本题考查双曲线的性质的综合应用,解题时要认真审题,注意函数的平移性质的灵活运用.

练习册系列答案
相关题目
下列四个数中,数值最小的是( )
| A、10111(2) |
| B、101(5) |
| C、25(10) |
| D、1B(16) |
等比数列的前n项,前2n项,前3n项的和分别是A,B,C,则( )
| A、(A+B)-C=B2 |
| B、A2+B2=A(B+C) |
| C、A+B=C |
| D、B2=AC |
cos17°sin43°+sin163°sin47°( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知集合A={x|x-2>0},B={1,2,3,4},则(∁RA)∩B=( )
| A、{1} |
| B、{1,2} |
| C、{2,3} |
| D、{2,3,4} |
一个几何体的三视图如图所示,则这个几何体的体积是( )
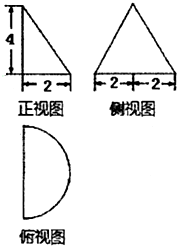

A、
| ||
B、
| ||
C、
| ||
D、
|
 甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,其中甲成绩的中位数为15,极差为12;乙成绩的众数为13,
甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,其中甲成绩的中位数为15,极差为12;乙成绩的众数为13,. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|