题目内容
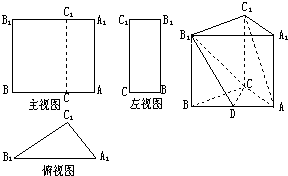已知三棱柱ABC-A1B1C1的三视图与直观图如图所示，其中主视图AA1B1B和左视图B1BCC1均为矩形，在俯视图△A1B1C1中，A1C1=3，A1B1=5，B1C1=4，（1）在三棱柱ABC-A1B1C1中，求证：BC⊥AC1；
（2）若三棱柱的高为5，求三视图中左视图的面积．
考点：简单空间图形的三视图
专题：空间位置关系与距离
分析：（1）因为主视图和左视图均为矩形、所以该三棱柱为直三棱柱，结合勾股定理可得BC⊥AC，进而由线面垂直的判定定理和性质得到BC⊥AC1；
（2）设左视图中BC的长等于底面△ABC中顶点C到边AB的距离d，求出d后，代入三角形面积公式，可得答案．
（2）设左视图中BC的长等于底面△ABC中顶点C到边AB的距离d，求出d后，代入三角形面积公式，可得答案．
解答：
证明：（1）因为主视图和左视图均为矩形、所以该三棱柱为直三棱柱，…2分
在俯视图△A1B1C1中，A1C1=3，A1B1=5，B1C1=4，
∴A1C12+B1C12=A1B12，
∴∠A1C1B1=90°，
∴BC⊥AC…4分
又∵BC⊥CC1，CC1∩A1C1=C1，
∴BC⊥平面ACC1A1．…6分
∵AC1?平面ACC1A1，
∴BC⊥AC1．…8分
解：（2）左视图中BC的长等于底面△ABC中顶点C到边AB的距离d，
d=
=
，…10分
∴左视图的面积S=
×5=12．…12分．
证明：（1）因为主视图和左视图均为矩形、所以该三棱柱为直三棱柱，…2分在俯视图△A1B1C1中，A1C1=3，A1B1=5，B1C1=4，
∴A1C12+B1C12=A1B12，
∴∠A1C1B1=90°，
∴BC⊥AC…4分
又∵BC⊥CC1，CC1∩A1C1=C1，
∴BC⊥平面ACC1A1．…6分
∵AC1?平面ACC1A1，
∴BC⊥AC1．…8分
解：（2）左视图中BC的长等于底面△ABC中顶点C到边AB的距离d，
d=
| 3×4 |
| 5 |
| 12 |
| 5 |
∴左视图的面积S=
| 12 |
| 5 |
点评：本题考查的知识点是简单空间图象的三视图，线面垂直与线线垂直的转化，是空间线面关系与三视图的简单综合应用，难度不大，属于基础题．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
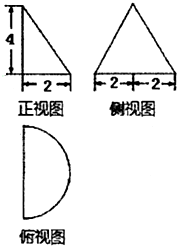
一个几何体的三视图如图所示，则这个几何体的体积是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，把边长为10的正六边形纸板剪去相同的六个角，做成一个底面为正六边形的无盖六棱柱盒子，设其高为h，体积为V（不计接缝）．