题目内容
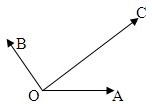
如图,已知|
|=2,|
|=1,|
|=4,
与
的夹角为120°,
与
的夹角为30°,用
,
表示
| OA |
| OB |
| OC |
| OA |
| OB |
| OA |
| OC |
| OA |
| OB |
| OC |

考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:如图所示,建立直角坐标系.C(2
,2),A(2,0),B(-
,
).设
=m
+n
,利用向量坐标运算、向量基本定理即可得出.
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| OC |
| OA |
| OB |
解答:
解:如图所示,建立直角坐标系.
C(2
,2),A(2,0),B(-
,
).
设
=m
+n
,
则(2
,2)=m(2,0)+n(-
,
).
∴2
=2m-
n,2=
n.
解得n=
,m=
.
∴
=
(
+
).

C(2
| 3 |
| 1 |
| 2 |
| ||
| 2 |
设
| OC |
| OA |
| OB |
则(2
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴2
| 3 |
| 1 |
| 2 |
| ||
| 2 |
解得n=
4
| ||
| 3 |
4
| ||
| 3 |
∴
| OC |
4
| ||
| 3 |
| OA |
| OB |
点评:本题考查了向量坐标运算、向量基本定理,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
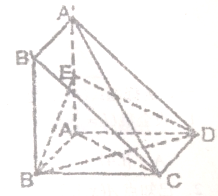 四边形ABCD与A′ABB′都是边长为a的正方形,且平面ABB′A′⊥平面ABCD,点E是A′A的中心.
四边形ABCD与A′ABB′都是边长为a的正方形,且平面ABB′A′⊥平面ABCD,点E是A′A的中心.