题目内容
抛物线y=x2-6x+5与x轴和y轴的交点所成的三角形的面积为 .
考点:二次函数的性质
专题:函数的性质及应用
分析:求出A(1,0),B(5,0),C(0,5),利用所成的三角形的面积为
|AB|×h求解即可.
| 1 |
| 2 |
解答:
解:∵抛物线y=x2-6x+5与x轴和y轴的交点,
A(1,0),B(5,0),C(0,5)
∴所成的三角形的面积为
|AB|×h=
×4×5=10,
故答案为:10.
A(1,0),B(5,0),C(0,5)
∴所成的三角形的面积为
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:10.
点评:本题考查了二次函数的性质,解析式的运用,属于容易题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
已知复数z满足:zi=2+i(i是虚数单位),则z的虚部为( )
| A、2i | B、-2i | C、2 | D、-2 |
从四面体的四个面中任意取出一个面,这个面的形状恰好为直角三角形的概率最大值为( )
| A、1 | ||
B、
| ||
C、
| ||
D、
|
已知椭圆
+
=1(a>b>0)的半焦距为c(c>0),左焦点为F,右顶点为A,抛物线y2=
(a+c)x与椭圆交于B、C两点,若四边形ABFC是菱形,则椭圆的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 15 |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知命题“若a,b,c成等比数列,则b2=ac”在它的逆命题、否命题,逆否命题中,真命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
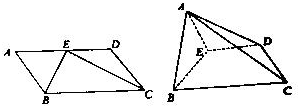 已知:平行四边形ABCD,AB=1,BC=2,∠BAD=60°,E为AD中点.将?ABCD沿BE折成直二面角.
已知:平行四边形ABCD,AB=1,BC=2,∠BAD=60°,E为AD中点.将?ABCD沿BE折成直二面角.