Question

10．某班54个学生中，参加美术课外活动小组的有32人，参加舞蹈课外活动小组的有24人，这两个课外活动小组都没有参加的有15人，从该班中任意抽取1名同学，他参加了两个课外活动小组的概率是多少？

Answer 1

分析 设两个课外活动小组都参加的人有x人，建立文氏图，得到15+（32-x）+（24-x）+x=54，求出x=17，有此能求出从该班中任意抽取1名同学，他参加了两个课外活动小组的概率．

解答 解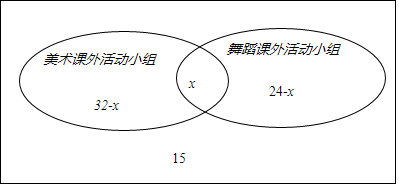：v某班54个学生中，参加美术课外活动小组的有32人，
参加舞蹈课外活动小组的有24人，这两个课外活动小组都没有参加的有15人，
设两个课外活动小组都参加的人有x人，
如图，建立文氏图，
∴15+（32-x）+（24-x）+x=54，
解得x=17，
∴从该班中任意抽取1名同学，他参加了两个课外活动小组的概率是p=$\frac{17}{54}$．

点评 本题考查概率的求法，考查古典概型、集合等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、分类与整合思想，是基础题．