题目内容
11.函数y=$\frac{1}{{x}^{2}+2x-8}$的单调递增区间是(-∞,-4),(-4,-1).分析 先求出函数定义域,然后对复合函数进行分解,再判定两简单函数的单调性,利用复合函数单调性的判定方法可得所求增区间
解答 解:由x2+2x-8≠0,得x≠2或x≠-4,
y=$\frac{1}{{x}^{2}+2x-8}$由y=$\frac{1}{u}$,u=x2+2x-8复合而成,
且y=$\frac{1}{u}$在每个象限内单调递减,
u=x2+2x-8在(-∞,-4),(-4,-1)上递减,在(-1,2),(2,+∞)上递增,
∴函数y=$\frac{1}{{x}^{2}+2x-8}$的单调递增区间是(-∞,-4),(-4,-1)
故答案为:(-∞,-4),(-4,-1)
点评 本题考查复合函数的单调性、幂函数、二次函数的单调性,属中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知圆(x-a)2+(y-b)2=r2(r>0)与x轴,y轴都相切.则a、b、r应满足条件( )
| A. | a=r,b=r | B. | |a|=|b|=r | C. | a=r | D. | b=r |
16.等差数列{an}的前n项为Sn,若公差d=-2,S3=21,则当Sn取得最大值时,n的值为( )
| A. | 10 | B. | 9 | C. | 6 | D. | 5 |
1.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{5}{4}$,且双曲线C的焦点到它的一条渐近线的距离为3,则双曲线C的方程为( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 |
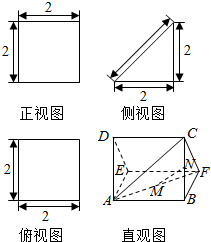 如图,多面体AED-BFC的直观图及三视图如图所示,M、N分别为AF、BC的中点.求证:
如图,多面体AED-BFC的直观图及三视图如图所示,M、N分别为AF、BC的中点.求证: