题目内容
设x1,x2是方程ax2+(b-1)x+1=0(a>0)的两个实根.
(1)若0<x1<2,x2-x1=2,求证:b<
;
(2)若x2-x1=2,x∈(x1,x2)时,求函数f(x)=-ax2-(b-1)x-1+2(x2-x)最大h(a)的最小值.
(1)若0<x1<2,x2-x1=2,求证:b<
| 1 |
| 4 |
(2)若x2-x1=2,x∈(x1,x2)时,求函数f(x)=-ax2-(b-1)x-1+2(x2-x)最大h(a)的最小值.
考点:一元二次方程的根的分布与系数的关系,二次函数的性质
专题:综合题,导数的综合应用
分析:(1)可根据韦达定理求出x1+x2和x1x2,根据已知|x2-x1|可以用x1+x2和x1x2,表示出来,从而求出b的范围;
(2)设f(x)=-ax2-(b-1)x-1+2(x2-x)=-a(x-x1)(x-x2)-2(x-x2)=-a(x-x2)(x-x1+
),再利用不等式进行放缩和利用导数进行求解.
(2)设f(x)=-ax2-(b-1)x-1+2(x2-x)=-a(x-x1)(x-x2)-2(x-x2)=-a(x-x2)(x-x1+
| 2 |
| a |
解答:
(1)证明:由题意,x1+x2=-
,x1x2=
两式相除得-(b-1)=
+
,即b=-(
+
)+1
当0<x1<2时,由x1x2=
>0,
∴x2-x1=2 即x2=x1+2
∴b=-
-
+1,x1∈(0,2)
令函数φ(x)=-
-
+1(x>0),则φ′(x)=
+
,
∴φ(x)在(0,+∞)上是增函数;
∴当x1∈(0,2)时,b=φ(x1)<φ(2)=-
-
+1=
,即b<
;
(2)解:∵x1,x2是方程ax2+(b-1)x+1=0(a>0)的两个实根,
∴可设f(x)=-ax2-(b-1)x-1+2(x2-x)=-a(x-x1)(x-x2)-2(x-x2)=-a(x-x2)(x-x1+
)
又x∈(x1,x2) 又a>0,
∴x-x1+
>0
∴g(x)=|a(x-x2)(x-x1+
)|=a(x2-x)(x-x1+
)
≤a(
)2=a(1+
)2=a+
+2
当且仅当x2-x1=x-x1+
即x=x1+1-
时取等号
∴h(a)=a+
+2,(a>0)
h′(a)=1-
<0
∴h(a)在(0,1)上是减函数,在(1,+∞)上是增函数.
∴h(a)min=h(1)=4.
| b-1 |
| a |
| 1 |
| a |
两式相除得-(b-1)=
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| x1 |
| 1 |
| x2 |
当0<x1<2时,由x1x2=
| 1 |
| a |
∴x2-x1=2 即x2=x1+2
∴b=-
| 1 |
| x1 |
| 1 |
| x1+2 |
令函数φ(x)=-
| 1 |
| x |
| 1 |
| x+2 |
| 1 |
| x2 |
| 1 |
| (x+2)2 |
∴φ(x)在(0,+∞)上是增函数;
∴当x1∈(0,2)时,b=φ(x1)<φ(2)=-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
(2)解:∵x1,x2是方程ax2+(b-1)x+1=0(a>0)的两个实根,
∴可设f(x)=-ax2-(b-1)x-1+2(x2-x)=-a(x-x1)(x-x2)-2(x-x2)=-a(x-x2)(x-x1+
| 2 |
| a |
又x∈(x1,x2) 又a>0,
∴x-x1+
| 2 |
| a |
∴g(x)=|a(x-x2)(x-x1+
| 2 |
| a |
| 2 |
| a |
≤a(
x2-x1+
| ||
| 2 |
| 1 |
| a |
| 1 |
| a |
当且仅当x2-x1=x-x1+
| 2 |
| a |
| 1 |
| a |
∴h(a)=a+
| 1 |
| a |
h′(a)=1-
| 1 |
| a2 |
∴h(a)在(0,1)上是减函数,在(1,+∞)上是增函数.
∴h(a)min=h(1)=4.
点评:主要考查函数与导数的综合应用能力,具体涉及到用导数来研究函数的单调性等基础知识,考查运算能力及用函数思想分析解决问题的能力.

练习册系列答案
相关题目
“m≥8”是“方程x2-mx+2m=0有两个大于2的根”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
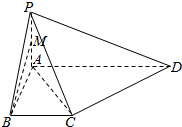 如图,已知PA⊥平面ABCD,AP=AB=BC=
如图,已知PA⊥平面ABCD,AP=AB=BC=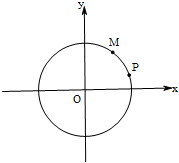 已知圆O:x2+y2=4.
已知圆O:x2+y2=4.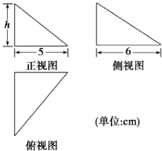 图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则h=
图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则h=