题目内容
已知函数f(x)=ln(1+x)-ln(1-x),有如下结论:
①?x∈(-1,1),有f(-x)=f(x);
②?x∈(-1,1),有f(-x)=-f(x);
③?x1,x2∈(-1,1),有
>0;
④?x1,x2∈(0,1),有f(
)≤
.
其中正确结论的序号是 .(写出所有正确结论的序号)
①?x∈(-1,1),有f(-x)=f(x);
②?x∈(-1,1),有f(-x)=-f(x);
③?x1,x2∈(-1,1),有
| f(x1)-f(x2) |
| x1-x2 |
④?x1,x2∈(0,1),有f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
其中正确结论的序号是
考点:对数函数的图像与性质,对数的运算性质
专题:函数的性质及应用
分析:函数f(x)是定义域(-1,1)上的奇函数,判断①错误,②正确;
根据f(x)是定义域(-1,1)上的增函数,判断③正确,
根据f(x)的图象在(0,1)上是向下凹的增函数,判断④正确.
根据f(x)是定义域(-1,1)上的增函数,判断③正确,
根据f(x)的图象在(0,1)上是向下凹的增函数,判断④正确.
解答:
解:∵函数f(x)=ln(1+x)-ln(1-x)=ln
,x∈(-1,1);
∴?x∈(-1,1),有f(-x)=ln
=ln(
)-1=-ln
=-f(x);
∴①错误,②正确;
又设x1,x2∈(-1,1),且x1<x2,
则f(x1)-f(x2)=ln
-ln
=ln
,
∵1-x1>1-x2>0,1+x2>1+x1>0,
∴0<
<1,
∴ln
<0,
∴f(x1)<f(x2),
∴f(x)是定义域(-1,1)上的增函数,
即?x1,x2∈(-1,1),有
>0,③正确;
又f(x)=ln(1+x)-ln(1-x),
求导得:f′(x)=
+
=
+
=
>0,
设g(x)=
,x∈(0,1),
再求导得:g′(x)=
>0,
∴f(x)是向下凹的增函数,
∴?x1,x2∈(0,1),有f(
)≤
,④正确.
综上,正确结论的序号是②③④.
故答案为:②③④.
| 1+x |
| 1-x |
∴?x∈(-1,1),有f(-x)=ln
| 1-x |
| 1+x |
| 1+x |
| 1-x |
| 1+x |
| 1-x |
∴①错误,②正确;
又设x1,x2∈(-1,1),且x1<x2,
则f(x1)-f(x2)=ln
| 1+x1 |
| 1-x1 |
| 1+x2 |
| 1-x2 |
| (1+x1)(1-x2) |
| (1-x1)(1+x2) |
∵1-x1>1-x2>0,1+x2>1+x1>0,
∴0<
| (1+x1)(1-x2) |
| (1-x1)(1+x2) |
∴ln
| (1+x1)(1-x2) |
| (1-x1)(1+x2) |
∴f(x1)<f(x2),
∴f(x)是定义域(-1,1)上的增函数,
即?x1,x2∈(-1,1),有
| f(x1)-f(x2) |
| x1-x2 |
又f(x)=ln(1+x)-ln(1-x),
求导得:f′(x)=
| 1 |
| 1+x |
| 1 |
| 1-x |
| 1-x |
| 1-x2 |
| 1+x |
| 1-x2 |
| 2 |
| 1-x2 |
设g(x)=
| 2 |
| 1-x2 |
再求导得:g′(x)=
| 4x |
| (1-x2)2 |
∴f(x)是向下凹的增函数,
∴?x1,x2∈(0,1),有f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
综上,正确结论的序号是②③④.
故答案为:②③④.
点评:本题考查了判断函数的奇偶性与单调性的应用问题,也考查了导数的应用问题,是综合性题目.

练习册系列答案
相关题目
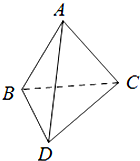 如图△ABCD和△BCD都是边长为2的正三角形,且二面角A-BC-D的大小为60°,则点的D到平面△ABC的距离为为( )
如图△ABCD和△BCD都是边长为2的正三角形,且二面角A-BC-D的大小为60°,则点的D到平面△ABC的距离为为( )