题目内容
已知圆O：x2+y2=4．（1）直线l1：
| 3 |
| 3 |
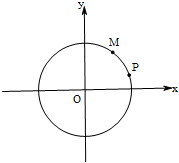
（2）如图，设M（x1，y1），P（x2，y2）是圆O上的两个动点，点M关于原点的对称点为M，点M关于x轴的对称点为M2，如果直线=PM1、PM2与y轴分别交于（0，m）和（0，n），问m•n是否为定值？若是求出该定值；若不是，请说明理由．
考点：平面向量的综合题
专题：综合题,直线与圆
分析：（1）先求出圆心（0，0）到直线
x+y-2
=0的距离，再利用弦长公式求得弦长AB的值．
（2）先求出M1和点M2的坐标，用两点式求直线PM1 和PM2的方程，根据方程求得他们在y轴上的截距m、n的值，计算mn的值，可得结论．
| 3 |
| 3 |
（2）先求出M1和点M2的坐标，用两点式求直线PM1 和PM2的方程，根据方程求得他们在y轴上的截距m、n的值，计算mn的值，可得结论．
解答：
解：（1）由于圆心（0，0）到直线
x+y-2
=0的距离d=
．
圆的半径r=2，∴|AB|=2
=2．…（4分）
（2）由于M（x1，y1）、P（x2，y2）是圆O上的两个动点，则可得M1（-x1，-y1）、M2（x1，-y1），且x12+y12=4，x22+y22=4．…（8分）
根据PM1的方程为
=
，令x=0求得y=m=
．
根据PM2的方程为
=
，令x=0求得y=n=
．…（12分）
∴mn=
•
=
=4为定值．…（14分）
| 3 |
| 3 |
| 3 |
圆的半径r=2，∴|AB|=2
| 4-3 |
（2）由于M（x1，y1）、P（x2，y2）是圆O上的两个动点，则可得M1（-x1，-y1）、M2（x1，-y1），且x12+y12=4，x22+y22=4．…（8分）
根据PM1的方程为
| y+y1 |
| y2+y1 |
| x+x1 |
| x2+x1 |
| x1y2-x2y1 |
| x2+x1 |
根据PM2的方程为
| y+y1 |
| y2+y1 |
| x-x1 |
| x2-x1 |
| -x1y2-x2y1 |
| x2-x1 |
∴mn=
| x1y2-x2y1 |
| x2+x1 |
| -x1y2-x2y1 |
| x2-x1 |
| x22(4-x12)-x12(4-x22) |
| x22-x12 |
点评：本题主要考查直线和圆相交的性质，点到直线的距离公式，用两点式求直线的方程、求直线在y轴上的截距，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目