题目内容
将函数f(x)=
+2的图象先向右平移
个单位,再向下平移两个单位,得到函数g(x)的图象.
(1)化简f(x)的表达式,并求出函数g(x)的表示式;
(2)指出函数g(x)在[-
,
]上的单调性和最大值;
(3)已知A(-2,
),B(2,
),问在y=g(x)的图象上是否存在一点P,使得
⊥
.
2
| ||
5+2cos2x-2
|
| π |
| 6 |
(1)化简f(x)的表达式,并求出函数g(x)的表示式;
(2)指出函数g(x)在[-
| π |
| 2 |
| π |
| 2 |
(3)已知A(-2,
| 3 |
| 2 |
| 9 |
| 2 |
| AP |
| BP |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)利用两角和公式和二倍角公式对函数解析式化简整理求得f(x)的表达式,进而通过图象的平移求得g(x)的解析式.
(2)对函数进行分类讨论,在x=±
,(-
,0],[0,
)上的最大值及单调性.
(3)以AB为直径作圆,利用g(x)的范围推断出g(x)与圆只有一个交点,进而求得P.
(2)对函数进行分类讨论,在x=±
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
(3)以AB为直径作圆,利用g(x)的范围推断出g(x)与圆只有一个交点,进而求得P.
解答:
解:(1)f(x)=
+2=
+2,
依题意g(x)=f(x-
)-2,
∴g(x)=
=
(2)g(±
)=0,
当x∈(-
,
)时,g(x)=
,
(i)当x∈(-
,
)时,1≥cosx>0
cosx+
≥2,当cosx=
时,等号成立,此时cosx=1,x=0
∴0<g(x)≤
,
∴g(x)的最大值为
,
令t=cosx,则0≤t<1,y=
+t
令t1>t2,则f(t1)-f(t2)=(t1-t2)+(
-
)=
<0,
∴函数y=
+t在(0,1)上单调减,
①在(-
,0)上y=cosx为增函数,y=t+
为减函数
∴y=cosx+
为减函数,则g(x)=
为增函数
②在[0,
)上y=cosx为减函数,y=t+
为减函数
则y=cosx+
为增函数,则g(x)=
为减函数
(3)∵由(1)知g(x)≤
,且g(0)=
,所以圆x2+(y-3)2=(
)2与y=g(x)图象有唯一交点P(0,
).
∴在y=g(x)图象上存在点P(0,
)使
⊥
.
2
| ||
5+2cos2x-2
|
2cos(x+
| ||
3+cos(2x+
|
依题意g(x)=f(x-
| π |
| 6 |
∴g(x)=
| 2cosx |
| 3+cos2x |
| cosx |
| cos2x+1 |
(2)g(±
| π |
| 2 |
当x∈(-
| π |
| 2 |
| π |
| 2 |
| 1 | ||
cosx+
|
(i)当x∈(-
| π |
| 2 |
| π |
| 2 |
cosx+
| 1 |
| cosx |
| 1 |
| cosx |
∴0<g(x)≤
| 1 |
| 2 |
∴g(x)的最大值为
| 1 |
| 2 |
令t=cosx,则0≤t<1,y=
| 1 |
| t |
令t1>t2,则f(t1)-f(t2)=(t1-t2)+(
| 1 |
| t1 |
| 1 |
| t2 |
| (t1-t2)(t1t2-1) |
| t1t2 |
∴函数y=
| 1 |
| t |
①在(-
| 1 |
| 2 |
| 1 |
| t |
∴y=cosx+
| 1 |
| cosx |
| 1 | ||
cosx+
|
②在[0,
| 1 |
| 2 |
| 1 |
| t |
则y=cosx+
| 1 |
| cosx |
| 1 | ||
cosx+
|
(3)∵由(1)知g(x)≤
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
∴在y=g(x)图象上存在点P(0,
| 1 |
| 2 |
| AP |
| BP |
点评:本题主要考查了三角函数恒等变换的应用,函数的单调性,复合函数的单调性等问题.注意符合函数在单调性上同增异减的口诀.

练习册系列答案
相关题目
函数f(x)=2x的反函数y=f-1(x)的图象是( )
A、 |
B、 |
C、 |
D、 |
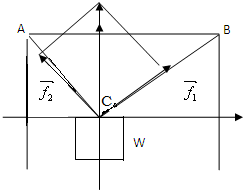 物体W的质量为50千克,用绳子将物体W悬挂在两面墙之间,已知两面墙之间的距离AB=10米(AB为水平线),AC=6米,BC=8米,求AC,BC上所受的力的大小.
物体W的质量为50千克,用绳子将物体W悬挂在两面墙之间,已知两面墙之间的距离AB=10米(AB为水平线),AC=6米,BC=8米,求AC,BC上所受的力的大小.