题目内容
19.已知函数f(x)=$sin(2x+\frac{π}{6})$(x∈R).(1)求函数f(x)的最小正周期和单调递增区间;
(2)求函数f(x)在区间$[{-\frac{π}{6},\frac{π}{6}}]$上的最大值和最小值.
分析 (1)利用周期公式求函数的最小正周期,将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间;
(2)x∈$[{-\frac{π}{6},\frac{π}{6}}]$上时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的最大值和最小值.
解答 解:函数f(x)=$sin(2x+\frac{π}{6})$(x∈R).
(1)函数f(x)的最小正周期T=$\frac{2π}{2}=π$;
令$-\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ$,k∈Z.
得:$-\frac{π}{3}+kπ$≤x≤$\frac{π}{6}+kπ$.
∴函数f(x)的单调递增区间为[$-\frac{π}{3}+kπ$,$\frac{π}{6}+kπ$],k∈Z.
(2)x∈$[{-\frac{π}{6},\frac{π}{6}}]$⇒$2x+\frac{π}{6}$∈[$-\frac{π}{6}$,$\frac{π}{2}$].
当$2x+\frac{π}{6}$=$-\frac{π}{6}$时,f(x)取得最小值为$-\frac{1}{2}$.
$2x+\frac{π}{6}$=$\frac{π}{2}$时,f(x)取得最大值为1.
∴函数f(x)在区间$[{-\frac{π}{6},\frac{π}{6}}]$上的最大值为1,最小值为$-\frac{1}{2}$.
点评 本题主要考查三角函数的图象和性质的运用,属于基础题.

练习册系列答案
相关题目
13.直线l在平面α内,直线m平行于平面α,且与直线l异面,动点P在平面α上,且到直线l、m距离相等,则点P的轨迹为( )
| A. | 直线 | B. | 椭圆 | C. | 抛物线 | D. | 双曲线 |
14.设$\overrightarrow{a}$,$\overrightarrow{b}$是非零向量,则“$\overrightarrow{a}$,$\overrightarrow{b}$共线”是“|$\overrightarrow{a}$|+|$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
14.公比为3的等比数列{an}的各项都是正数,且a1a5=9,则log3a6=( )
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
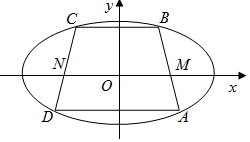 如图,已知中心在原点,焦点在x轴上的椭圆经过等腰梯形ABCD的四个顶点,两腰与x轴相交于点M,N,且$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$
如图,已知中心在原点,焦点在x轴上的椭圆经过等腰梯形ABCD的四个顶点,两腰与x轴相交于点M,N,且$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$