题目内容
8.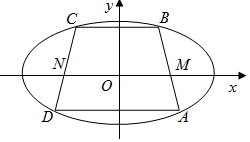 如图,已知中心在原点,焦点在x轴上的椭圆经过等腰梯形ABCD的四个顶点,两腰与x轴相交于点M,N,且$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$
如图,已知中心在原点,焦点在x轴上的椭圆经过等腰梯形ABCD的四个顶点,两腰与x轴相交于点M,N,且$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$(1)若等腰梯形的高等于3,上底BC=2,MN=6,求椭圆方程;
(2)当MN等于椭圆的短轴长时,求椭圆的离心率的取值范围.
分析 (1)根据向量的坐标运算,即可求得x2-3=-2(x1-3),y2=-2y1,根据单调性,即可求得A和B的坐标,代入椭圆方程,即可求得椭圆方程;
(2)由2x1+x2=3b,代入椭圆方程,由0<x2<b,即可求得3c2<2a2,根据椭圆的离心率公式,即可求得椭圆的离心率的取值范围.
解答  解:(1)由题意可知:设椭圆方程:mx2+ny2=1,
解:(1)由题意可知:设椭圆方程:mx2+ny2=1,
设A(x1,y1),B(x2,y2),由题意可知:点M坐标为(3,0),
则$\overrightarrow{MB}$=(x2-3,y2),$\overrightarrow{MA}$=(x1-3,y1),
由$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}$,则$\overrightarrow{MB}$=-2$\overrightarrow{MA}$,则x2-3=-2(x1-3),y2=-2y1,
由等腰梯形与椭圆的对称性,则y2-y1=3,x2=1,
∴x1=4,y1=-1,y2=2,
∴A(4,-1),B(1,2),
$\left\{\begin{array}{l}{16m+n=1}\\{m+4n=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=\frac{1}{21}}\\{n=\frac{5}{21}}\end{array}\right.$,
∴椭圆的标准方程:$\frac{{x}^{2}}{21}+\frac{5{y}^{2}}{21}=1$;
(2)由2x1+x2=3b,$\left\{\begin{array}{l}{\frac{{x}_{1}^{2}}{{a}^{2}}+\frac{{y}_{1}^{2}}{{b}^{2}}=1}\\{\frac{{x}_{2}^{2}}{{a}^{2}}+\frac{{y}_{2}^{2}}{{b}^{2}}=1}\end{array}\right.$,$\left\{\begin{array}{l}{\frac{{x}_{1}^{2}}{{a}^{2}}+\frac{{y}_{1}^{2}}{{b}^{2}}=1}\\{\frac{{x}_{2}^{2}}{{a}^{2}}+\frac{4{y}_{1}^{2}}{{b}^{2}}=1}\end{array}\right.$,消去y1,
4x12-x22=3a2,
∴2x1-x2=$\frac{{a}^{2}}{b}$,2x2=3b-$\frac{{a}^{2}}{b}$,
由0<x2<b,则0<3b2-a2<2b2,
∴a2<2a2,3c2<2a2,
∴e=$\frac{c}{a}$,则0<e<$\frac{\sqrt{6}}{3}$,
∴椭圆的离心率e的取值范围(0,$\frac{\sqrt{6}}{3}$).
点评 本题考查椭圆的标准方程及简单几何性质,椭圆的离心率的求法,考查椭圆的对称及等腰梯形的对称性,考查计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | $(0,\frac{π}{6}]$ | B. | $[\frac{π}{3},\frac{π}{2}]$ | C. | $(0,\frac{π}{3}]$ | D. | $[\frac{π}{3},π)$ |
| A. | -1或$\sqrt{3}$ | B. | 1或3 | C. | -2或6 | D. | 0或4 |
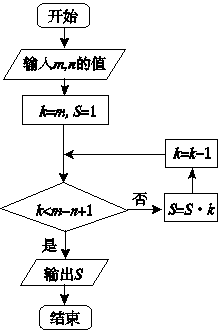
| A. | 7 | B. | 42 | C. | 210 | D. | 840 |
| A. | 正方形是平行四边形 | B. | 平行四边形的对角线相等 | ||
| C. | 正方形的对角线相等 | D. | 以上均不正确 |
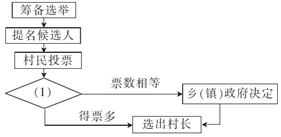 选举时常用的选举方式是差额选举(候选人多于当选人数),某村选举村长,具体方法是:筹备选举,由乡(镇)政府提名候选人,村民投票(同意,不同意,弃权),验票统计,得票多者选为村长;若票数相等,则由乡(镇)政府决定谁当选.下面的流程图表示该选举过程,则图(1)处应填的是验票统计.
选举时常用的选举方式是差额选举(候选人多于当选人数),某村选举村长,具体方法是:筹备选举,由乡(镇)政府提名候选人,村民投票(同意,不同意,弃权),验票统计,得票多者选为村长;若票数相等,则由乡(镇)政府决定谁当选.下面的流程图表示该选举过程,则图(1)处应填的是验票统计.