题目内容
已知函数f(x)=
(x≠-1),下列关于函数g(x)=[f(x)]2-f(x)+a(其中a为常数)的叙述中:
①?a>0,函数g(x)至少有4个零点;
②当a=0时,函数g(x)有5个不同零点;
③?a∈R,使得函数g(x)有6个不同零点;
④函数g(x)有多个不同零点的充要条件是0≤a≤
.
其中真命题有 .(把你认为的真命题的序号都填上)
| |x|(x+6) |
| x+1 |
①?a>0,函数g(x)至少有4个零点;
②当a=0时,函数g(x)有5个不同零点;
③?a∈R,使得函数g(x)有6个不同零点;
④函数g(x)有多个不同零点的充要条件是0≤a≤
| 1 |
| 4 |
其中真命题有
考点:命题的真假判断与应用,函数零点的判定定理
专题:阅读型,数形结合,函数的性质及应用
分析:画出函数f(x)的图象,令g(x)=0,由判别式小于0,可判断①;由f(x)=0,1,结合图象即可判断②;举a=
,解出f(x),结合图象,即可判断③;结合图象,a≥0,同时考虑判别式不小于0,即可求出充要条件,从而判断.
| 1 |
| 8 |
解答:
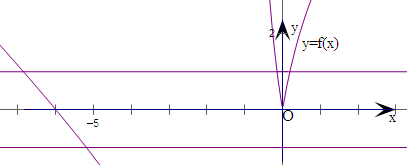 解:画出函数f(x)的图象:
解:画出函数f(x)的图象:
令g(x)=0,即
[f(x)]2-f(x)+a=0,
①若判别式小于0,即1-4a<0,
则方程无实根,函数g(x)无零点,故①错;
②a=0时,g(x)=0得f(x)=0或1,由图象显然有五个交点,即函数g(x)有5个不同零点,故②对;
③若a=
,则由g(x)=0得到f(x)=
或
,由图象可知有6个交点,故③对;
④函数g(x)有多个不同零点?g(x)=0有实根?a≥0且1-4a≥0?0≤a≤
.故④对.
故答案为:②③④.
 解:画出函数f(x)的图象:
解:画出函数f(x)的图象:令g(x)=0,即
[f(x)]2-f(x)+a=0,
①若判别式小于0,即1-4a<0,
则方程无实根,函数g(x)无零点,故①错;
②a=0时,g(x)=0得f(x)=0或1,由图象显然有五个交点,即函数g(x)有5个不同零点,故②对;
③若a=
| 1 |
| 8 |
2+
| ||
| 4 |
2-
| ||
| 4 |
④函数g(x)有多个不同零点?g(x)=0有实根?a≥0且1-4a≥0?0≤a≤
| 1 |
| 4 |
故答案为:②③④.
点评:本题考查函数的零点个数问题,转化为方程有无实根的问题,注意通过图象观察,考查数形结合的能力,属于中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
设a=cos1,b=cos3,c=cos5,则由如图算法输出值对应的是( )


| A、a | B、b | C、c | D、d |