题目内容
7.已知二次函数y=f(x)的定义域为R,f(x)在x=m时取得最值,又知y=g(x)为一次函数,且f(x)+g(x)=x2+x-2.(1)求f(x)的解析式,用m表示;
(2)当x∈[-2,1]时,f(x)≥-3恒成立,求实数m的取值范围.
分析 (1)直接利用在x=m处取得最值设出函数表达式,再利用y=g(x)为一次函数,且f(x)+g(x)=x2+x-2,求出a和b即可求f(x)的解析式.
(2)分别讨论给定区间与对称轴的位置关系,结合f(x)≥-3恒成立,综合讨论结果,可得实数m的取值范围.
解答 解:(1)设f(x)=a(x-m)2+b,
又f(x)+g(x)=x2+x-2,g(x)为一次函数,
∴a=1,则b=1-(1-m)2,
∴f(x)=(x-m)2+1-(1-m)2=(x-m)2-m2+2m.
(2)由函数f(x)=(x-m)2-m2+2m的图象是开口朝上,且以直线x=m为对称轴的抛物线,
且当x∈[-2,1]时,f(x)≥-3恒成立,则:
当m≤-2时,仅须f(-2)=6m+4≥-3,解得:m≥-$\frac{7}{6}$,此时不存在满足条件的m值;
当-2<m<1时,仅须f(m)=2m-m2≥-3,解得:-1≤m≤3,此时:-1≤m<1;
当m≥1时,仅须f(1)=1≥-3,解得:m≥1;
综上所述:m≥-1.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
2.若曲线C1:y=ax2(a>0)与曲线C2:y=e-x有公共切线,则a的取值范围为( )
| A. | [$\frac{{e}^{2}}{4}$,+∞) | B. | [$\frac{{e}^{2}}{8}$,+∞) | C. | (0,$\frac{{e}^{2}}{4}$] | D. | (0,$\frac{{e}^{2}}{8}$] |
16.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下:
已知y关于x的回归方程y=bx+1.05,则b=0.7.
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
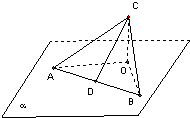 如图:已知三角形ABC,∠ACB=90°,AB在平面α内,C不在平面α内,点C在平面α内的射影为O,CA,CB与平面α所成角分别为30°,45°,CD⊥AB,D为垂足,则CD与平面α所成角60°.
如图:已知三角形ABC,∠ACB=90°,AB在平面α内,C不在平面α内,点C在平面α内的射影为O,CA,CB与平面α所成角分别为30°,45°,CD⊥AB,D为垂足,则CD与平面α所成角60°.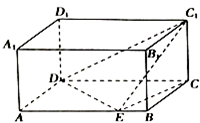 如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2,E是线段AB上的点,且EB=1,则二面角C-DE-C1的正切值为$\frac{\sqrt{2}}{2}$.
如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2,E是线段AB上的点,且EB=1,则二面角C-DE-C1的正切值为$\frac{\sqrt{2}}{2}$.