题目内容
12.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$为平面向量,且$\overrightarrow{a}$=(1,$\sqrt{2}$),$\overrightarrow{b}$=(x,y),|$\overrightarrow{b}$|=4.(1)若$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为150°,求|2$\overrightarrow{a}+\overrightarrow{b}$|及|$\overrightarrow{a}-2\overrightarrow{b}$|;
(2)若$\overrightarrow{b}$是与$\overrightarrow{a}$平行的向量,求$\overrightarrow{b}$的坐标.
分析 (1)根据向量的数量积公式和向量的模计算即可,
(2)根据向量的平行和向量的模得到关于x,y的方程组,解得即可.
解答 解:(1)易知$|\overrightarrow a|=\sqrt{3}$,$|2\overrightarrow a+\overrightarrow b{|^2}=4{\overrightarrow a^2}+4\overrightarrow a•\overrightarrow b+{\overrightarrow b^2}$
=$4×3+4×\sqrt{3}×4×cos{150°}+16$=12-24+16=4,
所以|2$\overrightarrow{a}+\overrightarrow{b}$|=2,
|$\overrightarrow{a}-2\overrightarrow{b}$|2=${\overrightarrow{a}}^{2}-4\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}$=3-4×4×$\sqrt{3}$×cos150°+4×16=91,
所以|$\overrightarrow{a}-2\overrightarrow{b}$|=$\sqrt{91}$
(2)由题意得:$\sqrt{2}x-y=0$,且x2+y2=16,
解得:$\left\{\begin{array}{l}{x=\frac{4\sqrt{3}}{3}}\\{y=\frac{4\sqrt{6}}{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{4\sqrt{3}}{3}}\\{y=-\frac{4\sqrt{6}}{3}}\end{array}\right.$
所以$\overrightarrow b=(\frac{{4\sqrt{3}}}{3},\frac{{4\sqrt{6}}}{3})$或$\overrightarrow b=(-\frac{{4\sqrt{3}}}{3},-\frac{{4\sqrt{6}}}{3})$
点评 本题考查了向量的数量积的运算和向量模的计算,以及向量平行,属于中档题.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案| A. | [$\frac{{e}^{2}}{4}$,+∞) | B. | [$\frac{{e}^{2}}{8}$,+∞) | C. | (0,$\frac{{e}^{2}}{4}$] | D. | (0,$\frac{{e}^{2}}{8}$] |
| X | 1 | 2 | 3 | 4 |
| P | 0.1 | 0.4 | 0.2 | 0.3 |
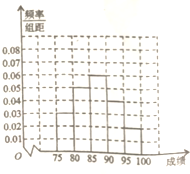 某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前100名学生,并对这100名学生按成绩分组(从低到高依次分为第1组、第2组、第3组、第4组、第5组),其频率分布直方图如图:现Q大学决定在第3、4、5组中用分层抽样的方法抽取6名学生进行面试,且本次面试中有B、C、D三位考官.
某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前100名学生,并对这100名学生按成绩分组(从低到高依次分为第1组、第2组、第3组、第4组、第5组),其频率分布直方图如图:现Q大学决定在第3、4、5组中用分层抽样的方法抽取6名学生进行面试,且本次面试中有B、C、D三位考官.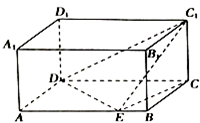 如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2,E是线段AB上的点,且EB=1,则二面角C-DE-C1的正切值为$\frac{\sqrt{2}}{2}$.
如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2,E是线段AB上的点,且EB=1,则二面角C-DE-C1的正切值为$\frac{\sqrt{2}}{2}$.