题目内容
17.函数f(x)=sin(ωx+$\frac{π}{6}$)(ω>0)的图象与x轴的交点横坐标构成一个公差为$\frac{π}{2}$的等差数列,要得到g(x)=cos(ωx+$\frac{π}{6}$)的图象,可将f(x)的图象( )| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向右平移$\frac{π}{2}$个单位 |
分析 由题意可得可得函数的周期为π,即$\frac{2π}{ω}$=π,求得ω=2,可得f(x)=sin(2x+$\frac{π}{6}$).再根据函数y=Asin(ωx+φ)的图象变换规律得出结论.
解答 解:根据函数f(x)=sin(ωx+$\frac{π}{6}$)(ω>0)的图象与x轴的交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列,可得函数的周期为π,
即:$\frac{2π}{ω}$=π,可得:ω=2,
可得:f(x)=sin(2x+$\frac{π}{6}$).
再由函数g(x)=cos(2x+$\frac{π}{6}$)=sin[$\frac{π}{2}$-(2x+$\frac{π}{6}$)]=sin[2(x+$\frac{π}{4}$)+$\frac{π}{6}$],
故把f(x)=sin(2x+$\frac{π}{6}$) 的图象向左平移$\frac{π}{4}$个单位,可得函数g(x)=cos(2x+$\frac{π}{6}$)的图象,
故选:B.
点评 本题主要考查等差数列的定义和性质,函数y=Asin(ωx+φ)的图象变换规律,考查了转化思想,属于基础题.

练习册系列答案
相关题目
19.已知角α的终边经过点P(-1,2),则tanα的值是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
2.若曲线C1:y=ax2(a>0)与曲线C2:y=e-x有公共切线,则a的取值范围为( )
| A. | [$\frac{{e}^{2}}{4}$,+∞) | B. | [$\frac{{e}^{2}}{8}$,+∞) | C. | (0,$\frac{{e}^{2}}{4}$] | D. | (0,$\frac{{e}^{2}}{8}$] |
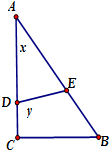 如图,在直角三角形ABC中,∠ACB=90°,AC=4,BC=3,点D,E分别线段AC,AB上,线段DE分三角形ABC为面积相等的两部分,设AD=x,DE=y.
如图,在直角三角形ABC中,∠ACB=90°,AC=4,BC=3,点D,E分别线段AC,AB上,线段DE分三角形ABC为面积相等的两部分,设AD=x,DE=y.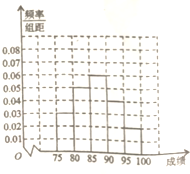 某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前100名学生,并对这100名学生按成绩分组(从低到高依次分为第1组、第2组、第3组、第4组、第5组),其频率分布直方图如图:现Q大学决定在第3、4、5组中用分层抽样的方法抽取6名学生进行面试,且本次面试中有B、C、D三位考官.
某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前100名学生,并对这100名学生按成绩分组(从低到高依次分为第1组、第2组、第3组、第4组、第5组),其频率分布直方图如图:现Q大学决定在第3、4、5组中用分层抽样的方法抽取6名学生进行面试,且本次面试中有B、C、D三位考官.