题目内容
10.如果一个点时一个指数函数和一个对数函数的图象的交点,那么称这个点为“好点”,下列四个点P1(1,1),P2(1,2),P3($\frac{1}{2}$,$\frac{1}{2}$),P4(2,2)中,“好点”的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 可设指数函数为y=ax,对数函数为y=logbx,容易判断P1,P2不在对数函数图象上,从而判断这两点不是“好点”,然后将P3的坐标分别代入指数函数和对数函数解析式,从而可解出a,b,进而判断出P3为“好点”,同样的方法可判断P4为好点,进而找出正确选项.
解答 解:设指数函数为y=ax,对数函数为y=logbx;
对于对数函数,x=1时,y=0,则P1,P2不是对数函数图象上的点;
∴P1,P2不是好点;
将P3的坐标分别代入指数函数和对数函数解析式得:
$\left\{\begin{array}{l}{{a}^{\frac{1}{2}}=\frac{1}{2}}\\{lo{g}_{b}\frac{1}{2}=\frac{1}{2}}\end{array}\right.$;
解得$a=b=\frac{1}{4}$;
即P3是指数函数$y=(\frac{1}{4})^{x}$和对数函数$y=lo{g}_{\frac{1}{4}}x$的交点,即P3为“好点”;
同样,将P4坐标代入函数解析式得:
$\left\{\begin{array}{l}{{a}^{2}=2}\\{lo{g}_{b}2=2}\end{array}\right.$;
解得$a=b=\sqrt{2}$;
∴P4是“好点”;
∴“好点”个数为2.
故选B.
点评 考查指数函数和对数函数解析式的一般形式,理解“好点”的定义,以及指数式和对数式的互化.

练习册系列答案
相关题目
12.设F1、F2是椭圆$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{2}$=1的两个焦点,点P在椭圆上,当△F1PF2的面积为2时,$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}$=( )
| A. | -$\frac{2\sqrt{6}}{3}$ | B. | 0 | C. | 1 | D. | $\frac{\sqrt{3}}{3}$ |
2.若曲线C1:y=ax2(a>0)与曲线C2:y=e-x有公共切线,则a的取值范围为( )
| A. | [$\frac{{e}^{2}}{4}$,+∞) | B. | [$\frac{{e}^{2}}{8}$,+∞) | C. | (0,$\frac{{e}^{2}}{4}$] | D. | (0,$\frac{{e}^{2}}{8}$] |
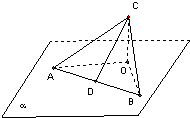 如图:已知三角形ABC,∠ACB=90°,AB在平面α内,C不在平面α内,点C在平面α内的射影为O,CA,CB与平面α所成角分别为30°,45°,CD⊥AB,D为垂足,则CD与平面α所成角60°.
如图:已知三角形ABC,∠ACB=90°,AB在平面α内,C不在平面α内,点C在平面α内的射影为O,CA,CB与平面α所成角分别为30°,45°,CD⊥AB,D为垂足,则CD与平面α所成角60°.