题目内容
已知函数f(x)=x-2
(1)求该函数的定义域;
(2)判断该函数的奇偶性,并证明.
(1)求该函数的定义域;
(2)判断该函数的奇偶性,并证明.
考点:函数奇偶性的判断,函数的定义域及其求法
专题:函数的性质及应用
分析:(1)根据函数成立的条件即可求函数的定义域.求该函数的定义域;
(2)根据函数奇偶性的定义进行判断.
(2)根据函数奇偶性的定义进行判断.
解答:
解:(1)∵f(x)=x-2=
,
∴要使函数有意义,则x≠0,
故函数的定义域为{x|x≠0},
(2)f(-x)=
=
=f(x),
则函数是偶函数.
| 1 |
| x2 |
∴要使函数有意义,则x≠0,
故函数的定义域为{x|x≠0},
(2)f(-x)=
| 1 |
| (-x)2 |
| 1 |
| x2 |
则函数是偶函数.
点评:本题主要考查函数的定义域的求解以及函数奇偶性的判断,比较基础.

练习册系列答案
相关题目
已知{an}是等差数列,Sn为其前n项和,若S4026-S1=0,O为坐标原点,点M(1,-a1)、N(2014,a2014),则
•
=( )
| OM |
| ON |
| A、0 | B、-1 |
| C、2014 | D、-2014 |
根据如下样本数据:
得到的回归方程为
=
x+
,则( )
| X | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 2 | -1 | 1 | -2 | -3 |
 |
| y |
 |
| b |
 |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
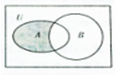
设全集U=R,A={x||x-1|<1},B={x|y=
},则图中阴影部分表示的集合是( )
| 1 | ||
|

| A、{x|x≥1} |
| B、{x|1≤x<2} |
| C、{x|0<x≤1} |
| D、{x|1≤1} |
在圆中有性质“半径为r的圆的面积为πr2”,类比圆的该条性质,在球中应有结论( )
A、半径为r的球的体积为
| ||
| B、半径为r的球的表面积为4πr2 | ||
| C、球心与截面圆圆心的连线垂直于截面 | ||
| D、与球心距离相等的两个截面圆面积相等 |