题目内容
9. 如图是计算1+3+5+…+99的程序框图,
如图是计算1+3+5+…+99的程序框图,(1)在框图的空白处填写适当的内容;
(2)用UNTIL语句编写程序.
分析 (1)分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S=1+3+5+…+99的值,由循环变量的初值为1,步长为2,由此易给出执行框中填写的语句.
(2)这是一个累加求和问题,可设计一个计数变量,一个累加变量,用循环结构实现这一算法.但要注意循环变量的初值、终值及步长的设置.
解答 解:(1)该程序框图的作用是累加并输出S=1+3+5+…+99的值,由计数变量的初值为1,步长为2,累加变量的初值为0,
从而可得应填入的条件是:
S=S+i
i=i+2
(2)程序如下:
S=0
i=1
DO
S=S+i
i=i+2
LOOP UNTIL i>99
PRINT S
END
点评 解决程序框图中的循环结构的问题,一般先按照框图的流程写出前几次循环的结果,然后找出规律再解决需解决的问题.算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,属于基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
19.(文科)学业水平考试后,某校对高二学生的数学、英语成绩进行了统计,结果如下(人数):
已知英语、数学的优秀率分别为24%、30%(注:合格人数中不包含优秀人数).
(1)求a、b的值;
(11)现按照英语成绩的等级,采用分层抽样的方法,从数学不合格的学生中选取6人,若再从这6人中任选2人,求这两名学生的英语成绩恰为一人优秀一人合格的概率.
| 项目 | 数学 | |||
| 优秀 | 合格 | 不合格 | ||
| 英 语 | 优秀 | 70 | 30 | 20 |
| 合格 | 60 | 240 | b | |
| 不合格 | a | 20 | 10 | |
(1)求a、b的值;
(11)现按照英语成绩的等级,采用分层抽样的方法,从数学不合格的学生中选取6人,若再从这6人中任选2人,求这两名学生的英语成绩恰为一人优秀一人合格的概率.
20.执行如图所示的程序框图.若输出的结果为3,则可输入的实数x的个数为( )
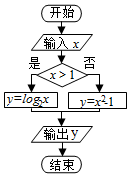

| A. | l | B. | 2 | C. | 3 | D. | 4 |
17.已知{an}是公差为$\frac{1}{2}$的等差数列,Sn为{an}的前n项和,若a2,a6,a14成等比数列,则S5=( )
| A. | $\frac{35}{2}$ | B. | 35 | C. | $\frac{25}{2}$ | D. | 25 |
14. 某校高三期中考试后,数学教师对本次全部数学成绩按 1:20进行分层抽样,随机抽取了 20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如下表所示的频率分布表:
某校高三期中考试后,数学教师对本次全部数学成绩按 1:20进行分层抽样,随机抽取了 20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如下表所示的频率分布表:
(Ⅰ)求表中 a,b 的值及成绩在[90,110)范围内的个体数,并估计这次考试全校高三数学成绩的及格率(成绩在[90,150]内为及格);
(Ⅱ)设茎叶图中成绩在[100,120)范围内的样本的中位数为m,若从成绩在[100,120)范围内的样品中每次随机抽取1个,每次取出不放回,连续取两次,求取出两个样本中恰好一个是数字m的概率.
 某校高三期中考试后,数学教师对本次全部数学成绩按 1:20进行分层抽样,随机抽取了 20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如下表所示的频率分布表:
某校高三期中考试后,数学教师对本次全部数学成绩按 1:20进行分层抽样,随机抽取了 20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如下表所示的频率分布表:| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150] | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
(Ⅱ)设茎叶图中成绩在[100,120)范围内的样本的中位数为m,若从成绩在[100,120)范围内的样品中每次随机抽取1个,每次取出不放回,连续取两次,求取出两个样本中恰好一个是数字m的概率.
1.圆(x+1)2+(y+2)2=4与圆(x-2)2+(y-2)2=9的公切线有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
18.在递增的等差数列{an}中,a1+a5=1,a2a4=-12,则公差d为( )
| A. | $\frac{7}{2}$ | B. | -$\frac{7}{2}$ | C. | $\frac{7}{2}$或-$\frac{7}{2}$ | D. | 7或-7 |
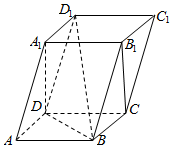 在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧面BCC1B1⊥底面ABCD,B1C=CD=2,BB1=2$\sqrt{2}$.
在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧面BCC1B1⊥底面ABCD,B1C=CD=2,BB1=2$\sqrt{2}$.