题目内容
1.若随机事件A在一次试验中发生的概率为p(0<p<1),用随机变量ξ表示A在一次试验发生的次数,则$\frac{4Dξ-1}{Eξ}$的最大值为( )| A. | 2 | B. | -1 | C. | 0 | D. | 1 |
分析 由已知得随机变量ξ的所有可能取值为0,1,且P(ξ=1)=p,P(ξ=0)=1-p,推导出 E(ξ)=p,D(ξ)=p-p2,从而得到$\frac{4Dξ-1}{Eξ}$=4-(4p+$\frac{1}{p}$),由此利用均值定理能求出$\frac{4Dξ-1}{Eξ}$的最大值.
解答 解:随机变量ξ的所有可能取值为0,1,
并且有P(ξ=1)=p,P(ξ=0)=1-p,
从而 E(ξ)=0×(1-p)+1×p=p,
D(ξ)=(0-p)2×(1-p)+(1-p)2×p=p-p2,
$\frac{4Dξ-1}{Eξ}$=$\frac{4(p-{p}^{2})-1}{p}$=4-(4p+$\frac{1}{p}$),
∵0<p<1,
∴4p+$\frac{1}{p}$$≥2\sqrt{4p×\frac{1}{p}}$=4,
当4p=$\frac{1}{p}$,p=$\frac{1}{2}$时,取“=”,
∴当p=$\frac{1}{2}$时,
$\frac{4Dξ-1}{Eξ}$取得最大值0.
故选:C.
点评 本题考查关于数学期望和方差的代数式的取大值的求法,是中档题,解题时要认真审题,注意离散型随机变量的数学期望与方差的性质的合理运用.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
12.不等式组$\left\{\begin{array}{l}{x+2y≥0}\\{x-3y≥0}\\{{x}^{2}+{y}^{2}≤4}\end{array}\right.$表示的平面区域的面积为( )
| A. | $\frac{π}{2}$ | B. | $\frac{3}{2}$π | C. | π | D. | 3π |
9.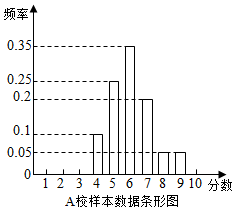 某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
B校样本数据统计表
(Ⅰ)计算两校样本数据的均值和方差,并根据所得数据进行比较.
(Ⅱ) 记事件C为“A校学生计算机优秀成绩高于B校学生计算机优秀成绩”.假设7分或7分以上为优秀成绩,两校学生计算机成绩相互独立.根据所给样本数据,以事件发生的频率作为相应事件发生的概率,求C的概率.
 某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:B校样本数据统计表
| 成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
(Ⅱ) 记事件C为“A校学生计算机优秀成绩高于B校学生计算机优秀成绩”.假设7分或7分以上为优秀成绩,两校学生计算机成绩相互独立.根据所给样本数据,以事件发生的频率作为相应事件发生的概率,求C的概率.
13.函数y=$\sqrt{4-{x}^{2}}$的定义域是( )
| A. | (-2,2) | B. | [-2,2] | C. | (-∞,-2) | D. | (2,+∞) |