题目内容
若方程
-
=1表示双曲线，则实数k的取值范围是（ ）
| x2 |
| 3-k |
| y2 |
| k-1 |
| A、k＜1 | B、1＜k＜3 |
| C、k＞3 | D、k＜1或k＞3 |
考点：双曲线的标准方程
专题：计算题,分类讨论,圆锥曲线的定义、性质与方程
分析：讨论双曲线的焦点位置，得到不等式，分别解出它们，再求并即可．
解答：
解：若方程
-
=1表示焦点在x轴上的双曲线，
则3-k＞0，且k-1＞0，解得1＜k＜3；
若方程
-
=1表示焦点在y轴上的双曲线，
则3-k＜0，且k-1＜0，解得k∈∅．
综上可得，1＜k＜3．
故选B．
| x2 |
| 3-k |
| y2 |
| k-1 |
则3-k＞0，且k-1＞0，解得1＜k＜3；
若方程
| x2 |
| 3-k |
| y2 |
| k-1 |
则3-k＜0，且k-1＜0，解得k∈∅．
综上可得，1＜k＜3．
故选B．
点评：本题考查双曲线的方程和性质，考查分类讨论的思想方法，考查运算能力，属于基础题．
练习册系列答案
相关题目
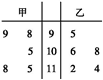在某中学举行的跳高比赛选拨赛中，甲和乙进行了5次比赛，他们的成绩用如图所示的茎叶图表示，则下列说法正确的是（ ）| A、甲的平均成绩比乙的平均成绩高，甲比乙成绩稳定 |
| B、甲的平均成绩比乙的平均成绩低，乙比甲成绩稳定 |
| C、甲的平均成绩与乙的平均成绩一样，但甲比乙成绩稳定 |
| D、甲的平均成绩与乙的平均成绩一样，但乙比甲成绩稳定 |
以下条件表达式正确的是（ ）
| A、1＜x＜2 | B、x＞＜1 |
| C、x＜＞1 | D、x≤1 |