题目内容

下列命题中，假命题为（　　）
A、若
a
-
b
=
0
，则
a
=
b
B、若
a
•
b
=0，则
a
=
0
或
b
=
0
C、若k∈R，k
a
=
0
，则k=0或 
a
=
0
D、若
a
，
b
都是单位向量，则
a
•
b
≤1恒成立
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量相等定义，即可判断A；运用向量的数量积的定义，即可判断B；
运用向量的数乘的定义，即可判断C；运用向量的数量积的定义和余弦函数的值域，即可判断D．
解答： 解：对于A．若
a
-
b
=
0
，则
a
=
b
，则A正确；
对于B．若
a
•
b
=0，则|
a
|•|
b
|•cos＜
a
，
b
＞=0，
则
a
=
0
或
b
=
0
或＜
a
，
b
＞=90°，则B错误；
对于C．若k
a
=
0
，则k=0或
a
=
0
，则C正确；
对于D．若
a
，
b
都是单位向量，
则
a
•
b
=1×1•cos＜
a
，
b
＞=cos＜
a
，
b
＞≤1，则D正确．
故选：B．
点评：本题考查向量的数量积的定义，考查向量相等的定义及向量的数乘的定义，考查余弦函数的值域，属于基础题和易错题．
练习册系列答案
相关题目
已知集合A={1，3，x}，B={x2，1}，使A∪B={1，3，x}成立的x值为
 
．
已知函数f（x）=lnx-
x2
2e2
+a（其中a∈R，无理数e=2.71828…）．当x=e时，函数f（x）有极大值
1
2
．
（1）求实数a的值；
（2）求函数f（x）的单调区间；
（3）任取x1，x2∈[e，e2]，证明：|f（x1）-f（x2）|＜3．
已知函数f（x）=2sin2（
π
4
+x）+
3
cos2x．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）若关于x的方程f（x）-m=2在x∈[0，
π
2
]上有两个不同的解，求实数m的取值范围．
确定下列三角函数值的符号：
（1）sin4；   
（2）cos5；   
（3）tan8；  
（4）tan（-3）．
已知等差数列{an}，a2=9，a5=21，
（1）求{an}的通项公式；
（2）令bn=2an，①证明{bn}是等比数列；②求数列{bn}的前n项和Sn．
设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（xi，yi）（i=1，2，…，n），用最小二乘法建立的回归方程为
y
=0.85x-85.71，则下列结论中不正确的是（　　）
A、若该大学某女生身高为170cm，则可断定其体重必为58.79kg
B、回归直线过样本点的中心（
.
x
，
.
y
）
C、若该大学某女生身高增加1cm，则其体重约增加0.85kg
D、y与x具有正的线性相关关系
用反证法证明命题：“已知a，b∈N，若ab不能被7整除，则a与b都不能被7整除”时，假设的内容应为（　　）
A、a，b都能被7整除
B、a，b不都能被7整除
C、a，b至少有一个能被7整除
D、a，b至多有一个能被7整除
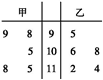在某中学举行的跳高比赛选拨赛中，甲和乙进行了5次比赛，他们的成绩用如图所示的茎叶图表示，则下列说法正确的是（　　）
A、甲的平均成绩比乙的平均成绩高，甲比乙成绩稳定
B、甲的平均成绩比乙的平均成绩低，乙比甲成绩稳定
C、甲的平均成绩与乙的平均成绩一样，但甲比乙成绩稳定
D、甲的平均成绩与乙的平均成绩一样，但乙比甲成绩稳定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网