Question

已知∠α和∠β满足sinα+2cosβ≤1且sinα-cosβ≤1，则sinα-2cosβ的最大值为

 

．

Answer 1

考点：同角三角函数基本关系的运用

专题：三角函数的求值

分析：设x=sinα，y=cosβ，则由题意可得

-1≤x≤1 -1≤y≤1 x+2y≤1 x-y≤1

，画出可行域，即图中阴影部分．目标函数z=x-2y，即y=

1

2

x-

z

2

，数形结合利用线性规划的知识求得z的最大值

解答： 解：设x=sinα，y=cosβ，则由题意可得

-1≤x≤1 -1≤y≤1 x+2y≤1 x-y≤1

，画出可行域，
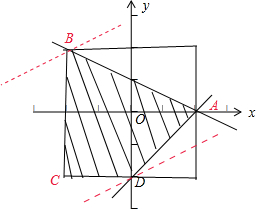
即图中阴影部分（四边形ABCD及其内部区域），A（1，0）、B（-1，1）、C（-1，-1）、D（0，-1）．
目标函数z=x-2y，即 y=

1

2

x-

z

2

，
显然，当直线 y=

1

2

x-

z

2

经过点（0，-1）时，函数z取得最大值为2．
即当sinα=0、cosβ=-1时，z=sinα-2cosβ取得最大值为2，
故答案为：2．

点评：本题主要考查求三角函数式的最值问题，简单的线性规划，体现了转化、数形结合的数学思想，属于中档题．